Coursera在线学习---第五节.Logistic Regression

一、假设函数与决策边界

---

---

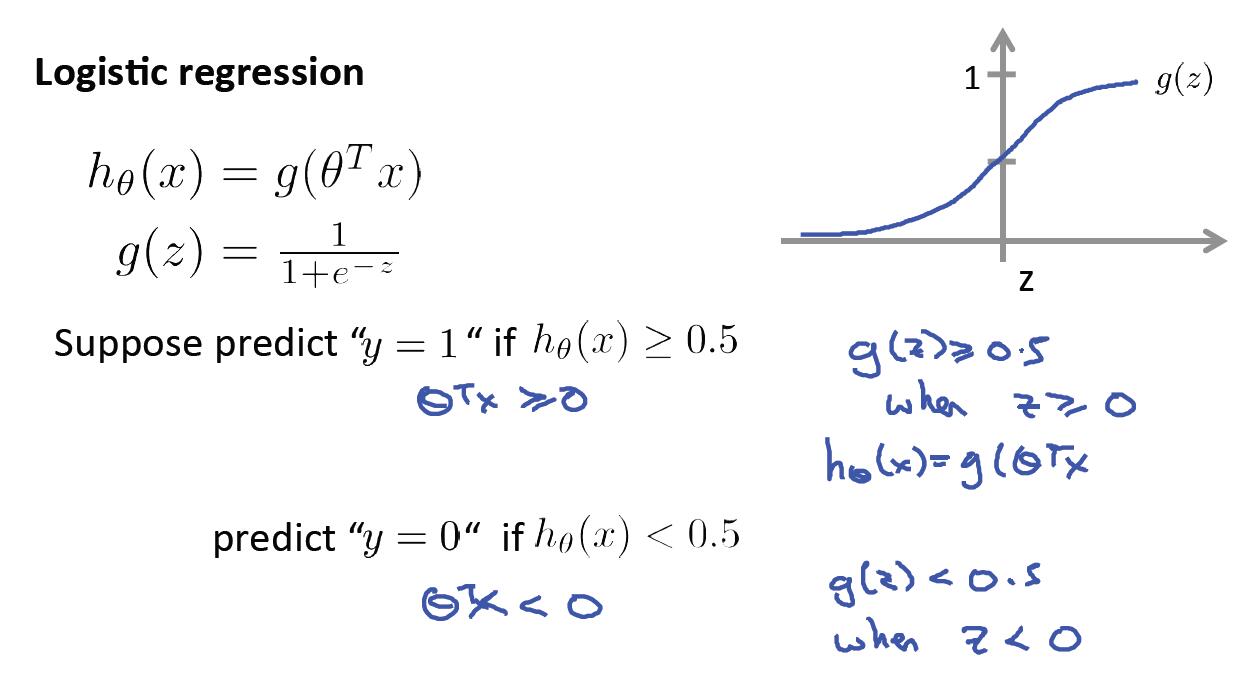
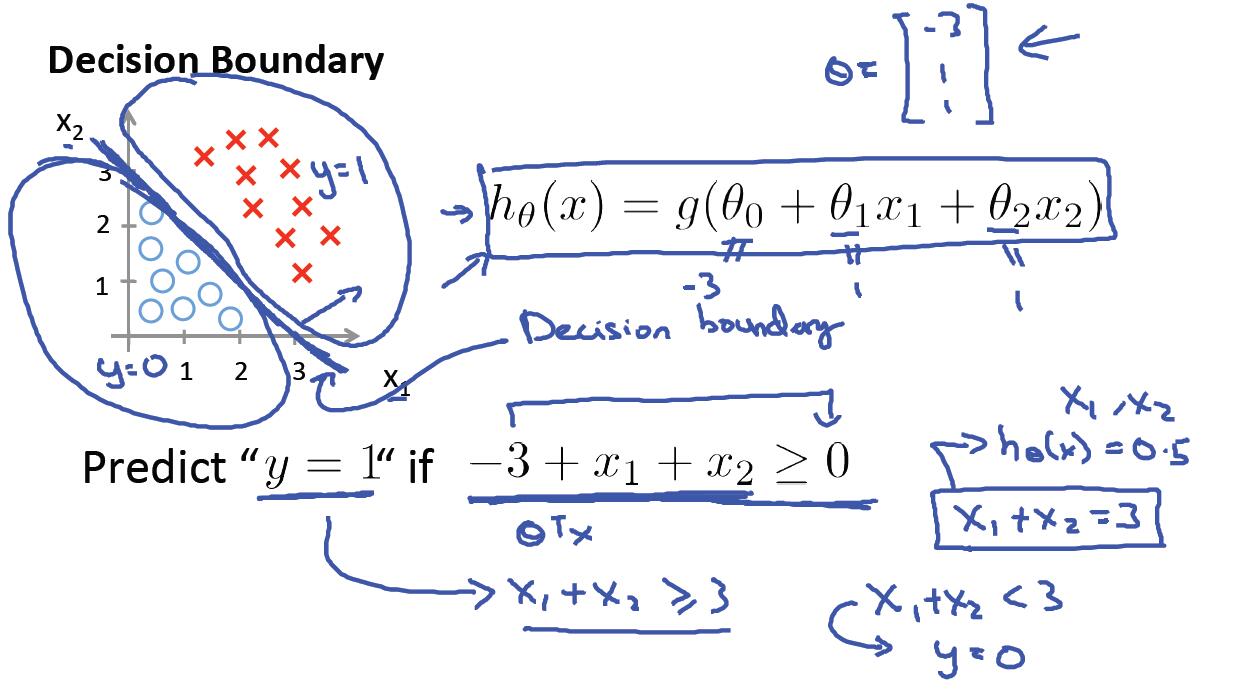
二、求解代价函数

---

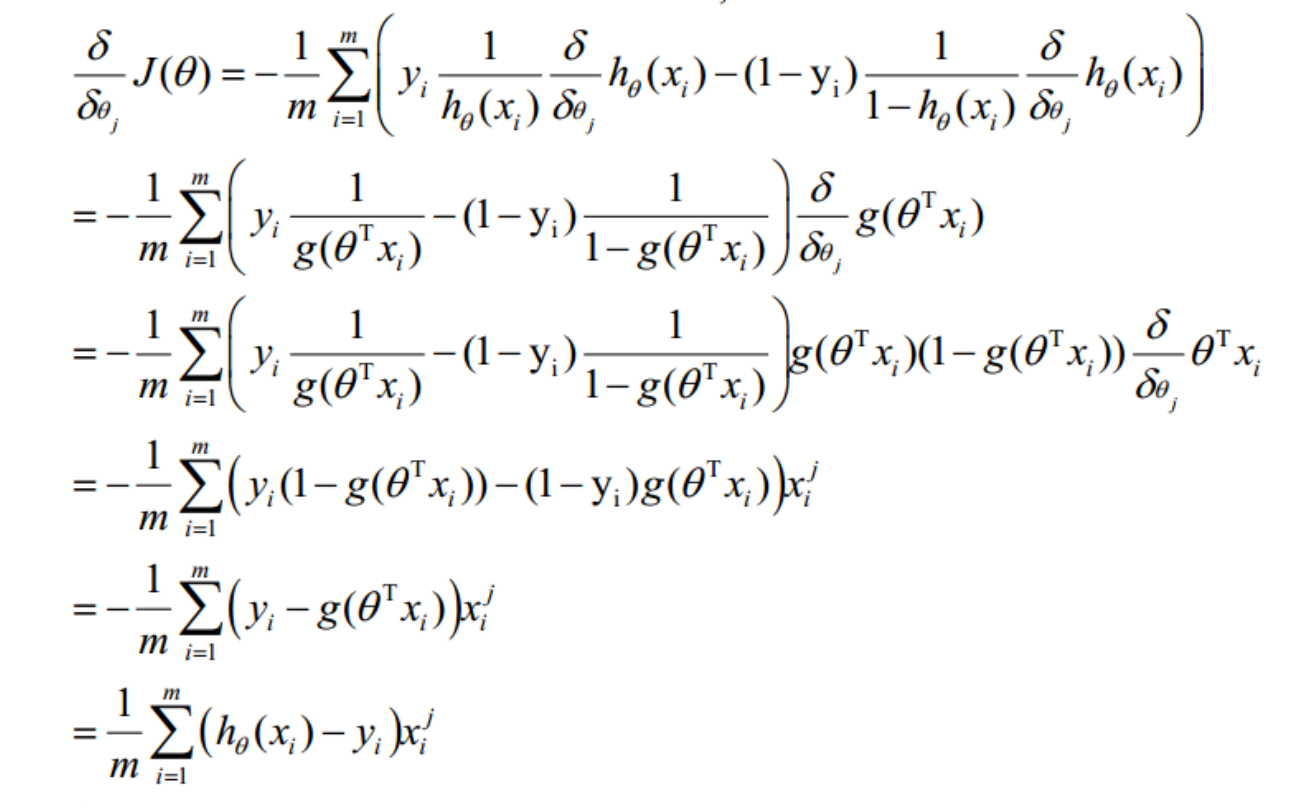
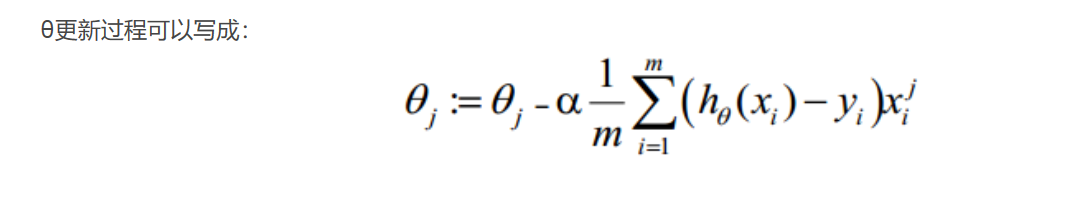
这样推导后最后发现，逻辑回归参数更新公式跟线性回归参数更新方式一摸一样。

为什么线性回归采用最小二乘法作为求解代价函数，而逻辑回归却用极大似然估计求解？

解答：

1）因为线性回归采用最小二乘法作为代价函数，这个函数是一个凸函数，能够得到全局最优解。如下图所示，因为其二阶导数在每个维度的偏导都是一个大于等于0的常数，满足凸函数的充要条件。

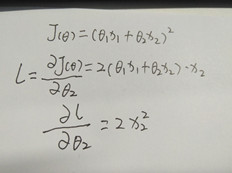
2）但是在逻辑回归中却会出现问题，因为将逻辑回归的表达式带入到最小二乘函数中得到的是一个非凸函数的图像，那么就会存在多个局部最优解，无法像凸函数一样得到全局最优解。怎么办呢？再换一个损失函数，对数损失函数，或者说是极大似然估计求解代价函数，两个是一个意思。经求其二阶偏导也是恒大于等于0的值，所以满足凸函数的充要条件，能求得全局最优解。

3）再一个使用平方损失函数，梯度更新的速度会和 sigmod 函数的梯度相关，经过推导公式发现梯度多了一个sigmoid的导数乘项g(x)*(1-g(x))，sigmod 函数在定义域内的梯度都不大于0.25，导致训练速度会非常慢。

4）采用极大似然估计想要让每一个 样本的预测都要得到最大的概率，即将所有的样本预测后的概率进行相乘都最大，也就是极大似然函数。

三、解决多分类问题

四、逻辑回归中Octave 一些实用指令

pos=find(y==1)   从y中查找出值为1的索引位置

mean(double(p==y))*100   计算预测的精确度(Accuracy)。double(p==y)将预测结果向量p与真实值向量y逐一对比，相同则置为1，不同则置为0，然后通过mean()函数计算一下均值，精确度就计算出来了。

double(p~=y) 向量p与真实值向量y逐一对比，相同则置为0，不同则置为1。与上述对比正好相反。

五、 常用的评价分类器性能的指标

• Precision：TP÷(TP+FP)，分类器预测出的正样本中，真实正样本的比例
• Recall：TP÷(TP+FN)，  在所有真实正样本中，分类器中能找到多少
• Accuracy：(TP+TN)÷(TP+NP+TN+FN)，分类器对整体的判断能力，即正确预测的比例