题解 洛谷 P6349 【[PA2011]Kangaroos】

先考虑对题目进行转化，我们称两个区间有交集为这两个区间能匹配，每个询问就是在序列中最长能连续匹配的长度。

对序列中的一个区间\([l,r]\)和询问的一个区间\([L,R]\)，若满足\(L \leqslant r\)且\(l \leqslant R\)，那么这两个区间是能匹配的。

可以将一个区间用点来表示，然后用\(K-D\ Tree\)来维护所有的询问区间，序列区间按顺序一个个去更新每个询问的匹配信息即可。

对\(K-D\ Tree\)中的维护一个矩形来考虑，比如下图的蓝色矩形为这个矩形。

当一个点落在红色矩形时，那么该点和矩形内的所有点都能匹配，对该矩形打上加法标记，使矩形内所有点的当前匹配数加一。

当一个点落在黄色矩形时，那么该点和矩形内的所有点都不能匹配，对该矩形打上清零标记，使矩形内所有点的当前匹配数清零。

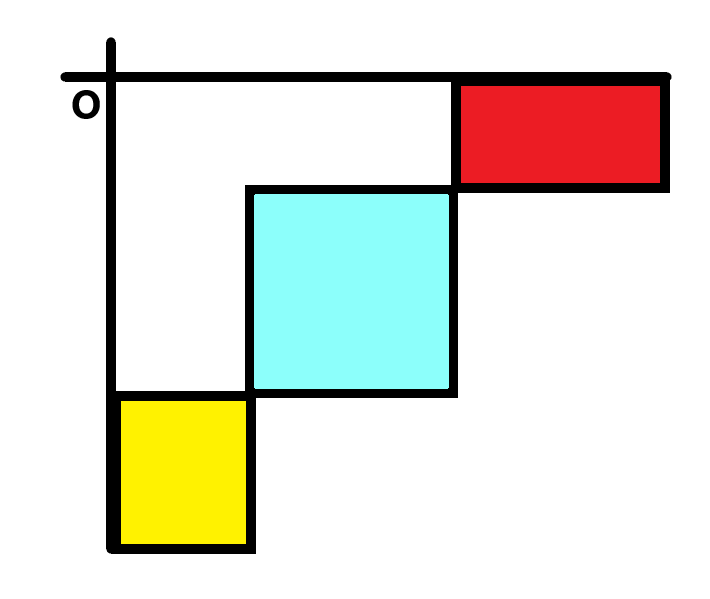
同时记录一个点在整个过程中的历史最大匹配数，其即为最终一个点所对应询问的答案。

对一个矩形清空后，还会进行一系列对其匹配数增加的操作，但此时打上加法标记是错误的，所以给它打上一个赋值标记，打标记时增加赋值标记即可，同时记录下这阶段赋值标记的历史最大值，并用其去更新该点的历史最大匹配数。

标记比较多，有很多细节，具体实现看代码吧。

\(code:\)

#include<bits/stdc++.h>
#define maxn 400010
using namespace std;
template<typename T> inline void read(T &x)
{
    x=0;char c=getchar();bool flag=false;
    while(!isdigit(c)){if(c=='-')flag=true;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    if(flag)x=-x;
}
int n,m,root,tot,type;
int cov[maxn],his[maxn],add[maxn],tag[maxn];
int ans[maxn],ma[maxn],cnt[maxn];
struct node
{
    int l,r;
}p[maxn];
struct KD_tree
{
    int d[2],mi[2],ma[2],ls,rs,id;
}t[maxn],dat[maxn];
bool cmp(const KD_tree &a,const KD_tree &b)
{
    return a.d[type]<b.d[type];
}
void pushup(int x)
{
    int ls=t[x].ls,rs=t[x].rs;
    for(int i=0;i<=1;++i)
    {
        t[x].ma[i]=t[x].mi[i]=t[x].d[i];
        if(ls)
        {
            t[x].ma[i]=max(t[x].ma[i],t[ls].ma[i]);
            t[x].mi[i]=min(t[x].mi[i],t[ls].mi[i]);
        }
        if(rs)
        {
            t[x].ma[i]=max(t[x].ma[i],t[rs].ma[i]);
            t[x].mi[i]=min(t[x].mi[i],t[rs].mi[i]);
        }
    }
}
void update(int x,int v)
{
    cnt[x]+=v,ma[x]=max(ma[x],cnt[x]);
}
void pushadd(int x,int v)
{
    update(x,v);
    if(cov[x]) tag[x]+=v,his[x]=max(his[x],tag[x]);
    else add[x]+=v;
}
void pushcov(int x)
{
    if(!cov[x]) cov[x]=1,his[x]=0;
    cnt[x]=tag[x]=0;
}
void pushtag(int x,int v1,int v2)
{
    cov[x]=1,his[x]=max(his[x],v2);
    cnt[x]=tag[x]=v1,ma[x]=max(ma[x],his[x]);
}
void pushdown(int x)
{
    int ls=t[x].ls,rs=t[x].rs;
    if(add[x])
    {
        pushadd(ls,add[x]),pushadd(rs,add[x]);
        add[x]=0;
    }
    if(cov[x])
    {
        pushtag(ls,tag[x],his[x]),pushtag(rs,tag[x],his[x]);
        cov[x]=tag[x]=0;
    }
}
void build(int l,int r,int k,int &x)
{
    x=++tot,type=k;
    int mid=(l+r)>>1;
    nth_element(dat+l+1,dat+mid+1,dat+r+1,cmp);
    t[x]=dat[mid];
    if(l<mid) build(l,mid-1,k^1,t[x].ls);
    if(r>mid) build(mid+1,r,k^1,t[x].rs);
    pushup(x);
}
bool in(KD_tree tr,int l,int r)
{
    return tr.ma[0]<=r&&l<=tr.mi[1];
}
bool out(KD_tree tr,int l,int r)
{
    return tr.mi[0]>r||l>tr.ma[1];
}
void modify(int x,int l,int r)
{
    int ls=t[x].ls,rs=t[x].rs;
    if(in(t[x],l,r))
    {
        pushadd(x,1);
        return;
    }
    if(out(t[x],l,r))
    {
        pushcov(x);
        return;
    }
    pushdown(x);
    if(t[x].d[0]<=r&&l<=t[x].d[1]) update(x,1);
    else cnt[x]=0;
    if(ls) modify(ls,l,r);
    if(rs) modify(rs,l,r);
}
void dfs(int x)
{
    int ls=t[x].ls,rs=t[x].rs;
    pushdown(x),ans[t[x].id]=ma[x];
    if(ls) dfs(ls);
    if(rs) dfs(rs);
}
int main()
{
    read(n),read(m);
    for(int i=1;i<=n;++i) read(p[i].l),read(p[i].r);
    for(int i=1;i<=m;++i)
        read(dat[i].d[0]),read(dat[i].d[1]),dat[i].id=i;
    build(1,m,0,root);
    for(int i=1;i<=n;++i) modify(root,p[i].l,p[i].r);
    dfs(root);
    for(int i=1;i<=m;++i) printf("%d\n",ans[i]);
    return 0;
}