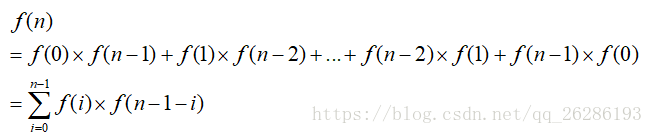【转】【数据结构】【有n个元素依次进栈,则出栈序列有多少种】

卡特兰数

大神解释：https://blog.csdn.net/akenseren/article/details/82149145      权侵删

原题

有一个容量足够大的栈，n个元素以一定的顺序入栈，出栈顺序有多少种？

比如，AB两个元素，入栈顺序为AB，出栈情况有两种：

（1）入A，出A，入B，出B，出栈顺序为AB；

（2）入A，入B，出B，出A，出栈顺序为BA。

因此，2个元素时，结果为2。

分析：设f(n)为“n个元素以一定的顺序入栈，出栈顺序的种类数”。显然f(1)=1,f(2)=2。我们现在来分析一般情况。一般情况下，我们可以按照“第一个入栈的元素，在出栈序列中的位置”作为分类手段。

举个例子，我们假设入栈元素为A，B，C，D。我们按照“A在出栈序列中的位置”分类讨论：

（1）当A第一个出栈时，A先进，然后马上出栈。这种情况下，共有“BCD出栈顺序的种类数”种方案。也就是f(n-1)。

（2）当A第二个出栈时，A先进，B再进，之后B需要马上出来（这样才能确保A排第二）。此时共有f(n-2)种方案。

（3）当A第三个出栈时，A先进，之后只要确保排在A后面两个的元素比A先出即可。此时共有f(2)*f(n-3)种方案。f(2)是指“BC入栈出栈顺序的种类数”，f(n-3)是指”D入栈出栈的种类数”。

……

分析到这里，规律就很显然了。

从第一项开始，分别是第一个入栈元素在第i+1个出栈的情况数。

上式中，令f(0)=1 。

这个实际上是卡特兰数（Catalan number，又称卡塔兰数）。

若编程实现，需要维护一个一维数组，时间复杂度为O(n^2)。（递归实现的时间复杂度太高）。

卡塔兰数的通项公式为h(n)=C(2n,n)-C(2n,n+1)(n=0,1,2,...)。

元素A、B、C、D依次进栈,写出所有可能的出栈序列

应该有14种情况
A第一个出栈：ABCD;ACBD;ACDB;ABDC;ADCB;

A第二个出栈：BACD;BADC;

A第三个出栈：CBAD;BCAD;

A第四个出栈：BCDA;CBDA;CDBA;BDCA;DCBA.

卡特兰数

　　卡特兰数前几项为 : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...

令h(0)=1,h(1)=1，catalan数满足递推式：　　h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)

例如：h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2　　

h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5　　

另类递推式：　　h(n)=h(n-1)*(4*n-2)/(n+1);　　

递推关系的解为：　　h(n)=C(2n,n)/(n+1) (n=1,2,3,...)　　

递推关系的另类解为：　　h(n)=c(2n,n)-c(2n,n+1)(n=1,2,3,...)

本题目的常规分析

首先，我们设f（n）=序列个数为n的出栈序列种数。同时，我们假定第一个出栈的序数是k。　　

第一个出栈的序数k将1~n的序列分成两个序列，其中一个是1~k-1，序列个数为k-1，另外一个是k+1~n，序列个数是n-k。　　

此时，我们若把k视为确定一个序数，那么根据乘法原理，f（n）的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数，即选择k这个序数的f（n）=f（k-1）×f（n-k）。而k可以选1到n，所以再根据加法原理，将k取不同值的序列种数相加，得到的总序列种数为：f（n）=f（0）f（n-1）+f（1）f（n-2）+……+f（n-1）f（0）。　　

看到此处，再看看卡特兰数的递推式，答案不言而喻，即为f（n）=h（n）= C（2n,n）/（n+1）= c（2n,n）-c（2n,n+1）（n=1，2，3，……）。　　

最后，令f（0）=1，f（1）=1。　

非常规分析

问题等价于：n个1和n个0组成一2n位的2进制数，要求从左到右扫描，1的累计数不小于0的累计数，试求满足这条件的数有多少？【对于每一个数来说，必须进栈一次、出栈一次。我们把进栈设为状态‘1’，出栈设为状态‘0’】
解答： 设P2n为这样所得的数的个数。在2n位上填入n个1的方案数为 C（n 2n）
不填1的其余n位自动填以数0。从C（n 2n）中减去不符合要求的方案数即为所求。
不合要求的数指的是从左而右扫描，出现0的累计数超过1的累计数的数。

不合要求的数的特征是从左而右扫描时，必然在某一奇数2m+1位上首先出现m+1个的累计数，和m个1的累计数。
此后的2（n－m）－1位上有n－m个1，n－m－1个0。如若把后面这部分2（n－m）－1位，0与1交换【就是0换成1 1换成0 不是顺序的调换 是数值换】，使之成为n－m个0，n－m－1个1，结果得 1个由n＋1个0和n－1个1组成的2n位数，即一个不合要求的数对应于一个由n－1个0和n＋1个1组成的一个排列。

我们把进栈设为状态‘1’，出栈设为状态‘0’。【对于每一个数来说，必须进栈一次、出栈一次】
由于任意时刻，出栈的操作数一定不超过入栈的操作数

不符合要求的数的特征是由左而右扫描时，必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数，
【出栈数已经大于入栈数了】【因为合法的排列 无论在哪个位置 1都是>=0的】【前面m个位置0、1排列不管怎么排列都已经不合法）】
此后的2(n-m)-1位上有n-m个1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换，使之成为n-m个0和n-m-1个1，
结果得1个由n+1个0和n-1个1组成的2n位数，即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。
卡特兰数 为什么要0 1 互换？【互换后的排列中0比1多1个，那么不管怎么排列，也都不合法】

类似问题 买票找零

1.有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)

最终结果：C(2n,n)-C(2n,n+1)

2.

*

* *

* * *

* * * *

* * * * *

形如这样的直角三角形网格，从左上角开始，只能向右走和向下走，问总共有多少种走法？

问题的由来：编号为 1 到 n 的 n 个元素，顺序的进入一个栈，则可能的出栈序列有多少种？

对问题的转化与思考：n 个元素进栈和出栈，总共要经历 n 次进栈和 n 次出栈。这就相当于对这 2n 步操作进行排列。

一个模型：一个 n*n 的正方形网格，从左上角顶点到右下角顶点，只能向右走和向下走。问共有多少种走法。如果将向右走对应上述问题的出栈，向下走对应上述问题的进栈，那么，可 以视此模型为对上述问题的具体描述。而解决此问题，只要在总共从左上角到右下角的2n步中，选定向右走的步数，即共有C(n 2n)种走法。

但是存在一个问题，如果走法越过了对角线，那么对应到上述问题是出栈数比入栈数多，这是不符合实际的。

对以上模型进行处理，对角线将以上正方形网格分成两部分，只留下包含对角线在内的下半部分，那么就不会出现越过对角线的问题。而这问题就是开始提出的问题。

 

3.在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?

https://blog.csdn.net/hackbuteer1/article/details/7450250 没懂