各种优化方法总结比較（sgd/momentum/Nesterov/adagrad/adadelta）

前言

这里讨论的优化问题指的是，给定目标函数f(x)，我们须要找到一组參数x。使得f(x)的值最小。

本文下面内容如果读者已经了解机器学习基本知识，和梯度下降的原理。

SGD

SGD指stochastic gradient descent，即随机梯度下降。是梯度下降的batch版本号。

对于训练数据集，我们首先将其分成n个batch，每一个batch包括m个样本。我们每次更新都利用一个batch的数据。而非整个训练集。

即：

xt+1=xt+Δxt

Δxt=−ηgt

当中。η为学习率，gt为x在t时刻的梯度。

这么做的优点在于：

• 当训练数据太多时。利用整个数据集更新往往时间上不显示。batch的方法能够降低机器的压力，而且能够更快地收敛。

• 当训练集有非常多冗余时（相似的样本出现多次），batch方法收敛更快。以一个极端情况为例。若训练集前一半和后一半梯度同样。那么如果前一半作为一个batch，后一半作为还有一个batch。那么在一次遍历训练集时，batch的方法向最优解前进两个step，而总体的方法仅仅前进一个step。

Momentum

SGD方法的一个缺点是，其更新方向全然依赖于当前的batch。因而其更新十分不稳定。

解决这一问题的一个简单的做法便是引入momentum。

momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向。同一时候利用当前batch的梯度微调终于的更新方向。

这样一来，能够在一定程度上添加稳定性，从而学习地更快，而且还有一定摆脱局部最优的能力：

Δxt=ρΔxt−1−ηgt

当中，ρ 即momentum，表示要在多大程度上保留原来的更新方向，这个值在0-1之间，在训练開始时，因为梯度可能会非常大，所以初始值一般选为0.5；当梯度不那么大时，改为0.9。η 是学习率，即当前batch的梯度多大程度上影响终于更新方向，跟普通的SGD含义同样。ρ 与 η 之和不一定为1。

Nesterov Momentum

这是对传统momentum方法的一项改进，由Ilya Sutskever(2012 unpublished)在Nesterov工作的启示下提出的。

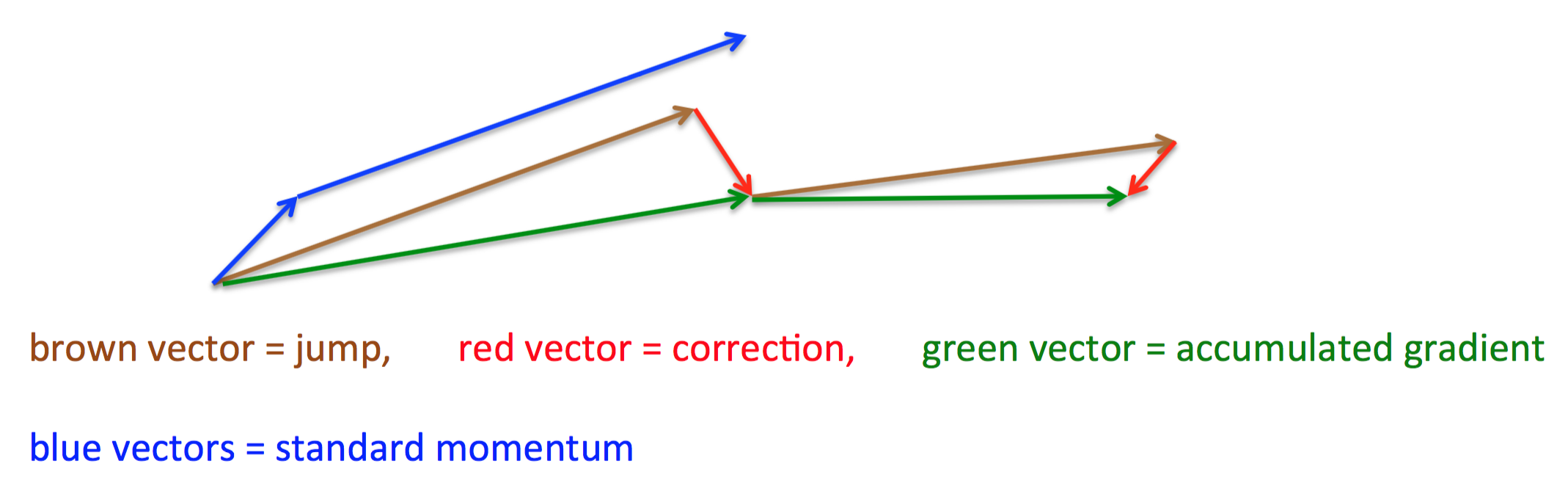
其基本思路例如以下图（转自Hinton的coursera公开课lecture 6a）：

首先，依照原来的更新方向更新一步（棕色线）。然后在该位置计算梯度值（红色线），然后用这个梯度值修正终于的更新方向（绿色线）。

上图中描写叙述了两步的更新示意图。当中蓝色线是标准momentum更新路径。

公式描写叙述为：

Δxt=ρΔxt−1−ηΔf(xt+ρΔxt−1)

Adagrad

上面提到的方法对于全部參数都使用了同一个更新速率。可是同一个更新速率不一定适合全部參数。比方有的參数可能已经到了仅须要微调的阶段。但又有些參数因为相应样本少等原因，还须要较大幅度的调动。

Adagrad就是针对这一问题提出的，自适应地为各个參数分配不同学习率的算法。其公式例如以下：

Δxt=−η∑tτ=1g2τ+ϵ‾‾‾‾‾‾‾‾‾‾‾√gt

当中gt 同样是当前的梯度，连加和开根号都是元素级别的运算。eta 是初始学习率。因为之后会自己主动调整学习率，所以初始值就不像之前的算法那样重要了。而ϵ是一个比較小的数，用来保证分母非0。

其含义是，对于每一个參数。随着其更新的总距离增多，其学习速率也随之变慢。

Adadelta

Adagrad算法存在三个问题

• 其学习率是单调递减的，训练后期学习率非常小
• 其须要手工设置一个全局的初始学习率
• 更新xt时。左右两边的单位不同一

Adadelta针对上述三个问题提出了比較美丽的解决方式。

首先，针对第一个问题，我们能够仅仅使用adagrad的分母中的累计项离当前时间点比較近的项，例如以下式：

E[g2]t=ρE[g2]t−1+(1−ρ)g2t

Δxt=−ηE[g2]t+ϵ‾‾‾‾‾‾‾‾‾‾√gt

这里ρ是衰减系数，通过这个衰减系数。我们令每一个时刻的gt随之时间依照ρ指数衰减。这样就相当于我们仅使用离当前时刻比較近的gt信息。从而使得还非常长时间之后，參数仍然能够得到更新。

针对第三个问题，事实上sgd跟momentum系列的方法也有单位不统一的问题。sgd、momentum系列方法中：

Δx的单位∝g的单位∝∂f∂x∝1x的单位

相似的，adagrad中，用于更新Δx的单位也不是x的单位。而是1。

而对于牛顿迭代法：

Δx=H−1tgt

当中H为Hessian矩阵。因为其计算量巨大。因而实际中不常使用。其单位为：

Δx∝H−1g∝∂f∂x∂2f∂2x∝x的单位

注意，这里f无单位。因而，牛顿迭代法的单位是正确的。

所以，我们能够模拟牛顿迭代法来得到正确的单位。注意到：

Δx=∂f∂x∂2f∂2x⇒1∂2f∂2x=Δx∂f∂x

这里，在解决学习率单调递减的问题的方案中，分母已经是∂f∂x的一个近似了。这里我们能够构造Δx的近似，来模拟得到H−1的近似，从而得到近似的牛顿迭代法。详细做法例如以下：

Δxt=−E[Δx2]t−1‾‾‾‾‾‾‾‾‾√E[g2]t+ϵ‾‾‾‾‾‾‾‾‾‾√gt

能够看到，如此一来adagrad中分子部分须要人工设置的初始学习率也消失了，从而顺带攻克了上述的第二个问题。

各个方法的比較

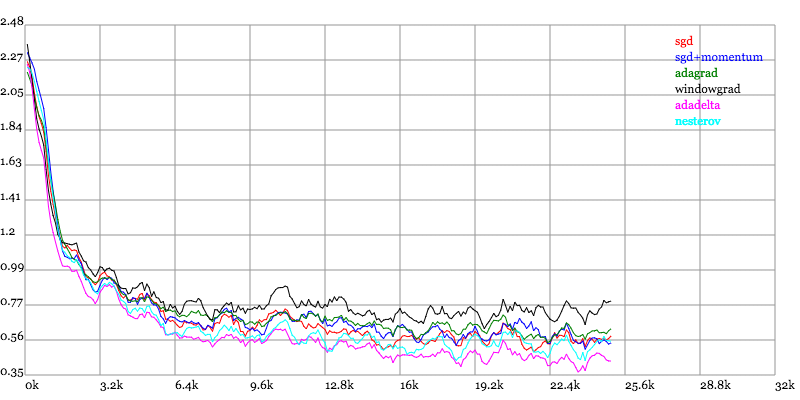
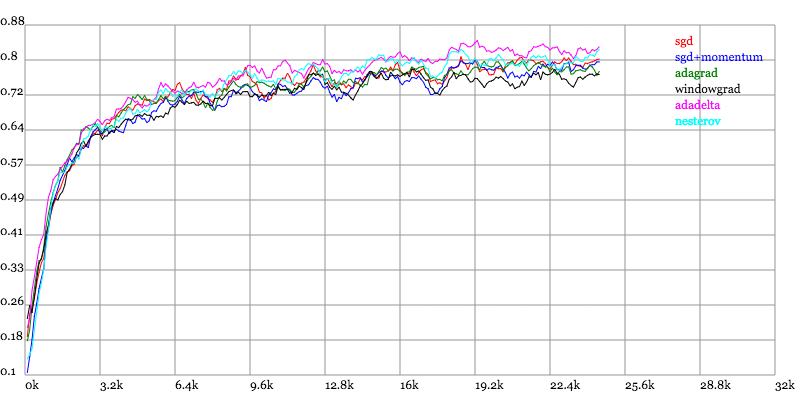
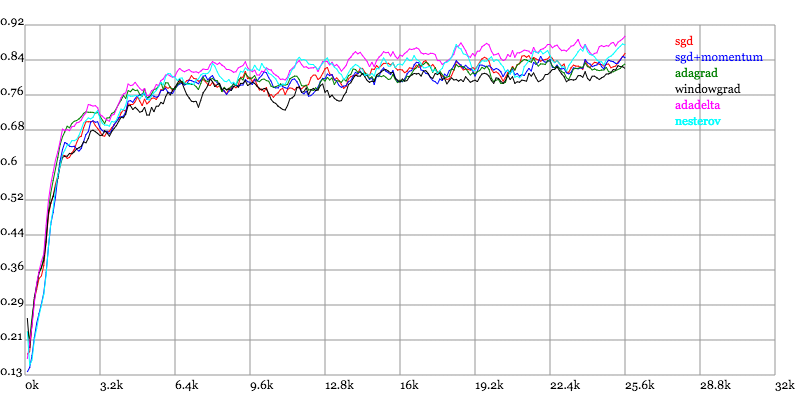
Karpathy做了一个这几个方法在MNIST上性能的比較，其结论是：

adagrad相比于sgd和momentum更加稳定，即不须要怎么调參。而精调的sgd和momentum系列方法不管是收敛速度还是precision都比adagrad要好一些。

在精调參数下，一般Nesterov优于momentum优于sgd。而adagrad一方面不用怎么调參，还有一方面其性能稳定优于其它方法。

实验结果图例如以下：

Loss vs. Number of examples seen

Testing Accuracy vs. Number of examples seen

Training Accuracy vs. Number of examples seen

其它总结文章

近期看到了一个非常棒的总结文章，除了本文的几个算法。还总结了RMSProp跟ADAM（当中ADAM是眼下最好的优化算法，不知道用什么的话用它就对了）