机器学习理论基础学习14.2---线性动态系统-粒子滤波 particle filter

一、背景

与卡曼滤波不同的是，粒子滤波假设隐变量之间（隐变量与观测变量之间）是非线性的，并且不满足高斯分布，可以是任意的关系。

求解的还是和卡曼滤波一样，但由于分布不明确，所以需要用采样的方法求解。

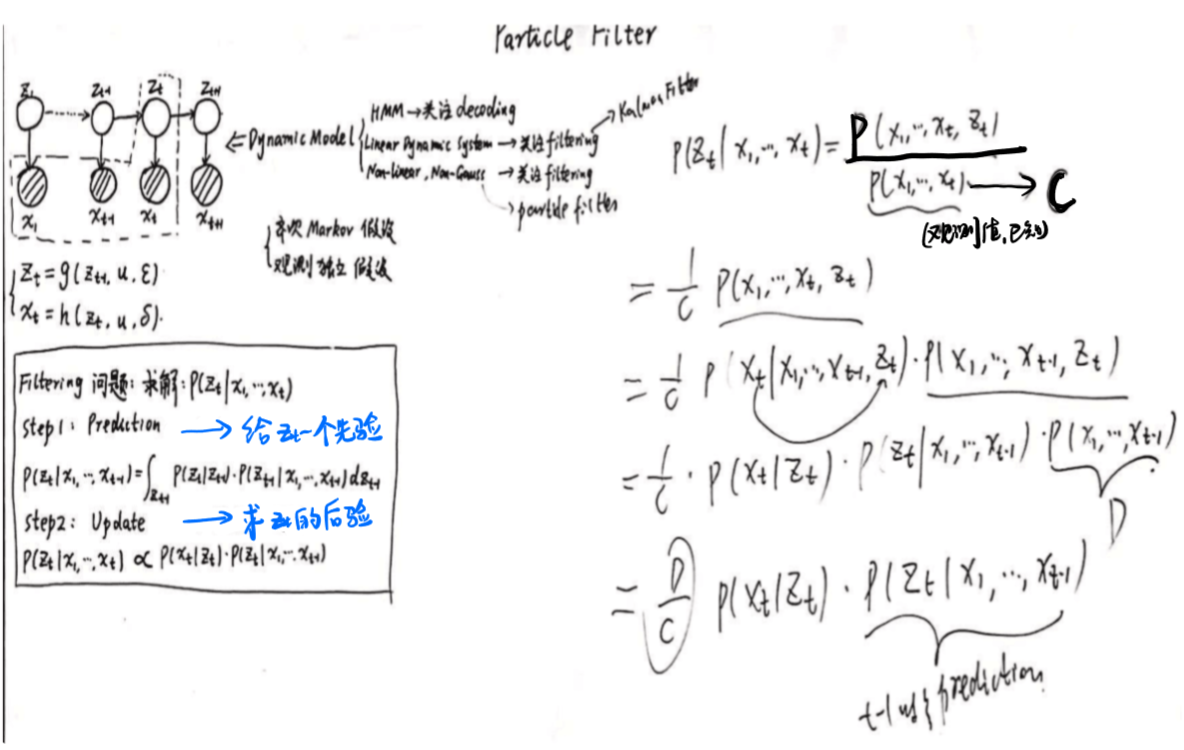
二、重要性采样（importance sampling & SIS）

重要性采样（IS）需要计算p(zt|x1,...,t), t与t-1之间没有递推关系，不易求解

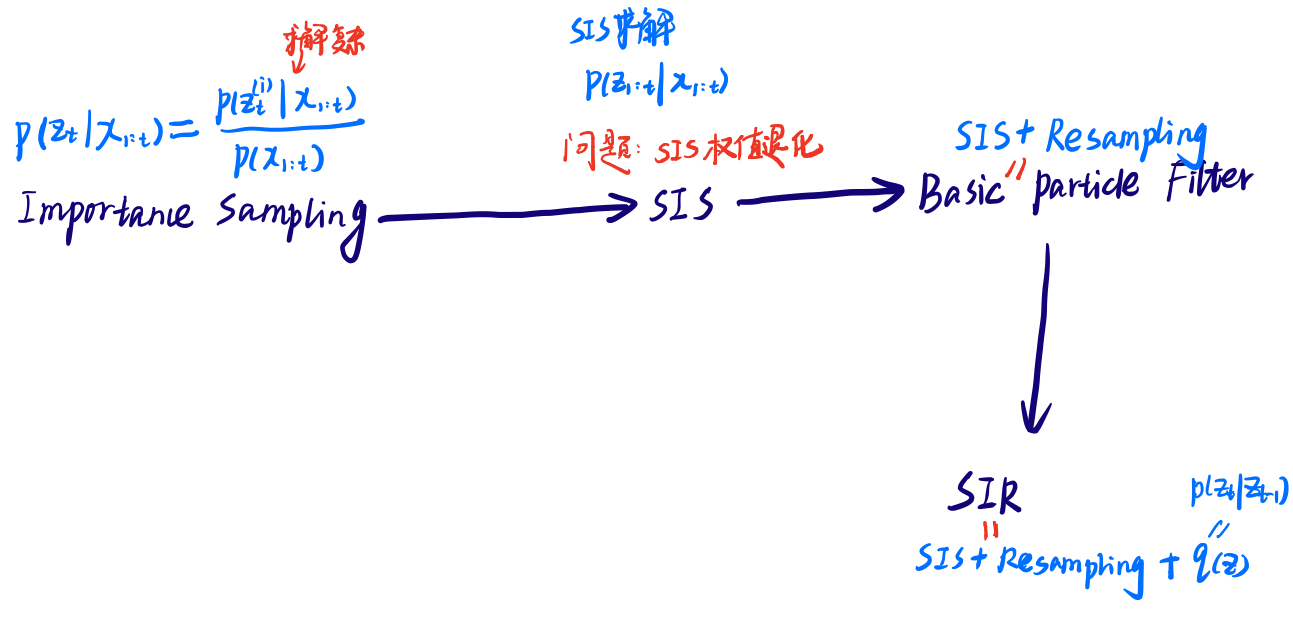
为此引入SIS，转换成求解p(z1,...t|x1,...t)，且能够推出递推关系，方便求解

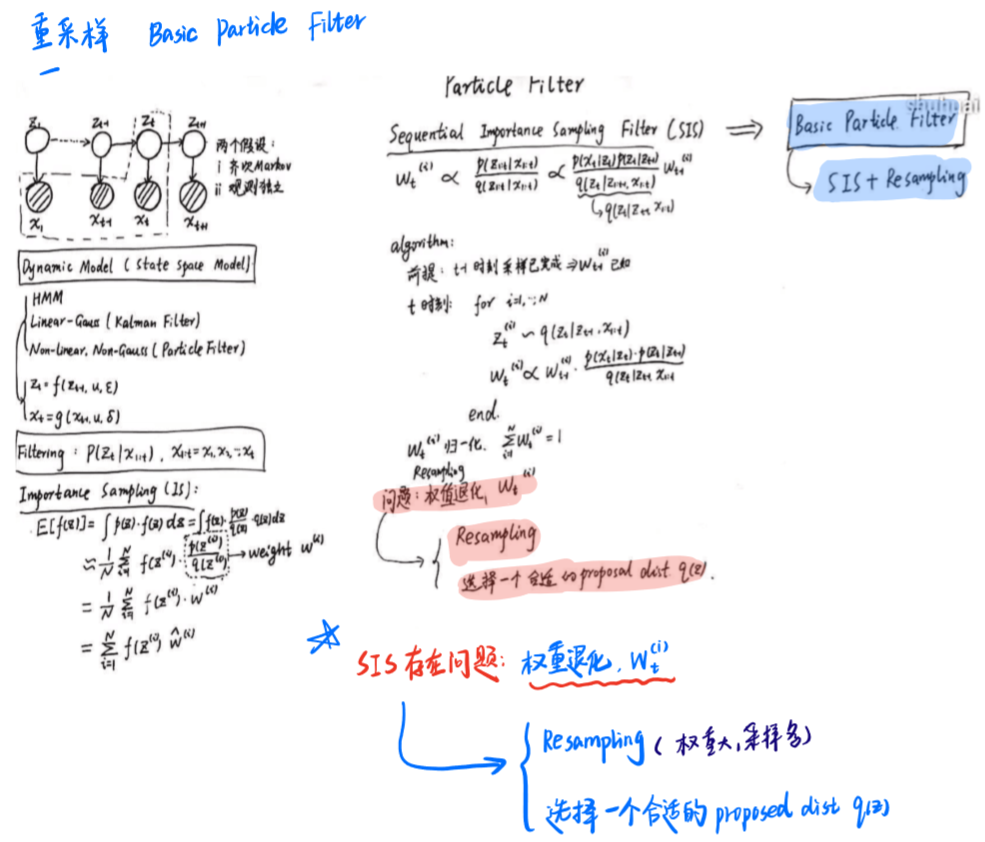
三、重采样Basic Particle Filter

但SIS也有一个严重问题，权重会随着时间增长呈指数递减。

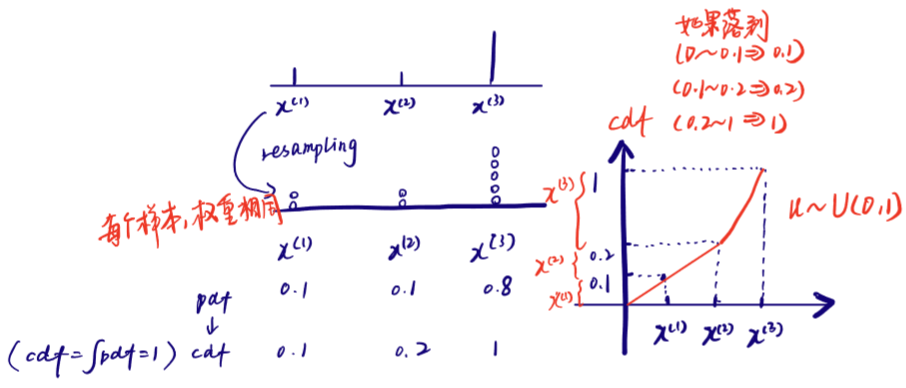
为此引入Basic particle filter = SIS + Resampling（权重大的，多采样）

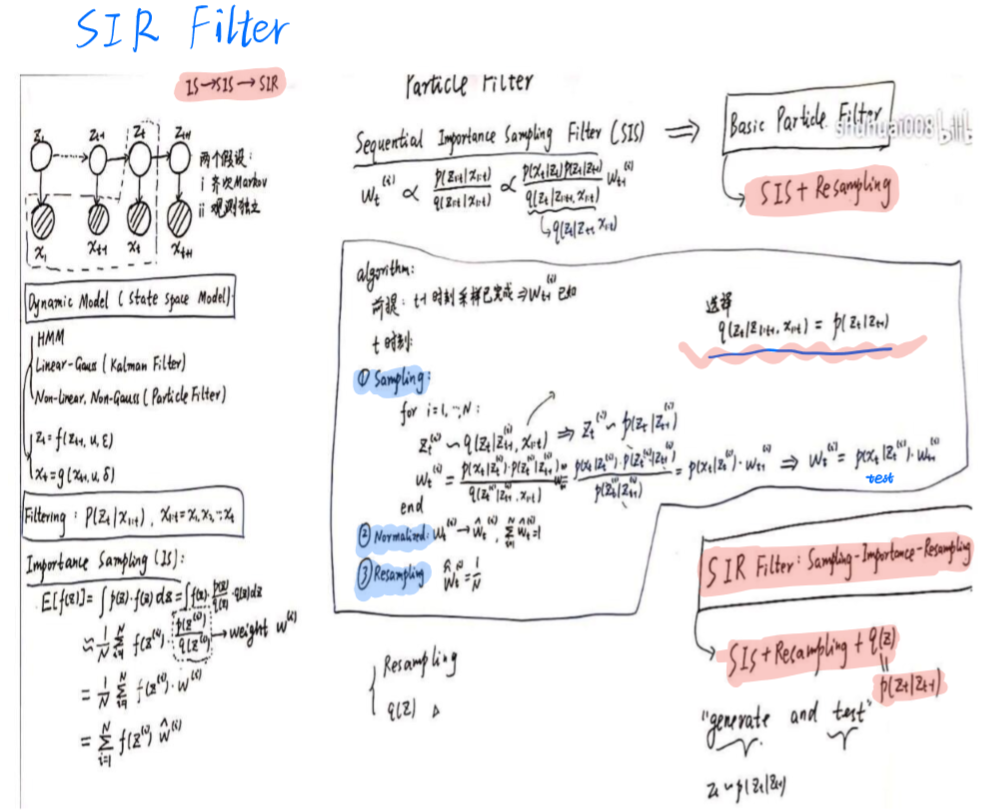
四、SIR Filter

SIR filter与basic particle filter区别在于，选择q(zt|z1,...,zt-1,x1,...,xt) = p(zt|zt-1)

SIR filter = SIS + resampling + q(z)