sklearn交叉验证2-【老鱼学sklearn】

过拟合

过拟合相当于一个人只会读书，却不知如何利用知识进行变通。

相当于他把考试题目背得滚瓜烂熟，但一旦环境稍微有些变化，就死得很惨。

从图形上看，类似下图的最右图：

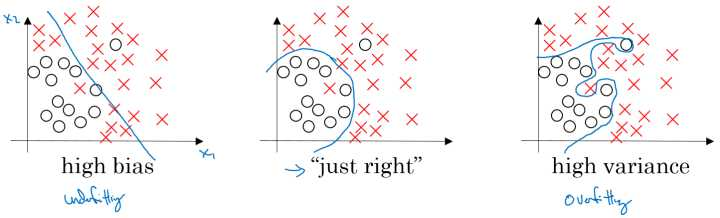
从数学公式上来看，这个曲线应该是阶数太高的函数，因为一般任意的曲线都能由高阶函数来拟合，它拟合得太好了，因此丧失了泛化的能力。

用Learning curve 检视过拟合

首先加载digits数据集，其包含的是手写体的数字，从0到9：

# 加载数据
digits = load_digits()
X = digits.data
y = digits.target

然后用SVC(支持向量机)对手写体数字进行分类，当然，这里要介绍的核心函数是learning_curve，先上代码看看：

# 导入支持向量机
from sklearn.svm import SVC
model = SVC(gamma=0.001)

train_sizes, train_loss, test_loss = learning_curve(model, X, y, cv=10, scoring='neg_mean_squared_error', train_sizes=[0.1, 0.25, 0.5, 0.75, 1])
# 平均每一轮所得到的平均方差(共5轮，分别为样本10%、25%、50%、75%、100%)
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)

在learning_curve中设置了十一法的数据，同时在打分时使用了neg_mean_squared_error方式，也就是方差值，因此这个最后的得分值是负数；train_sizes指定了5轮检视学习曲线(10%, 25%, 50%, 75%, 100%):

最后，我们把根据每轮的训练集大小对于最终得分的影响程度画个图，相当于做题数量的多少跟最终考试成绩的关系图：

# 可视化图形
import matplotlib.pyplot as plt
plt.plot(train_sizes, train_loss_mean, label="Train")
plt.plot(train_sizes, test_loss_mean, label="Test")
plt.legend()
plt.show()

显示图形为：

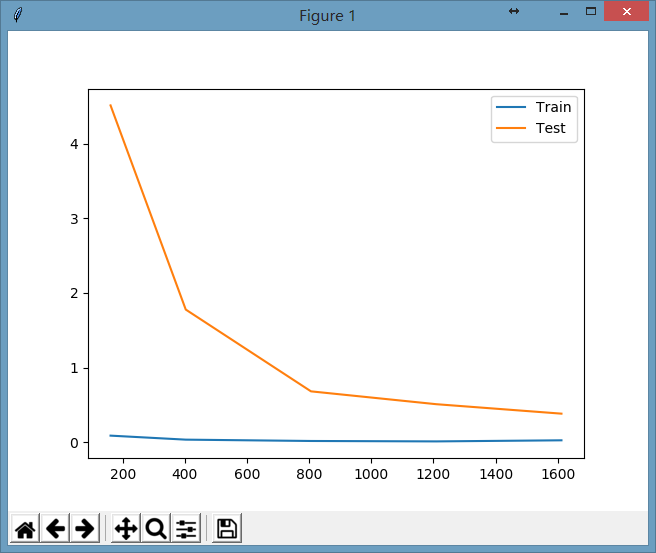
看起来随着做题数量的增加，考试成绩越来越好了（损失函数的值越来越小了），并且考试成绩在慢慢逼近平常的训练成绩。

完整的代码如下：

from sklearn.datasets import load_digits

# 加载数据
digits = load_digits()
X = digits.data
y = digits.target

# 加载学习曲线模块
from sklearn.model_selection import learning_curve
import numpy as np

# 导入支持向量机
from sklearn.svm import SVC
model = SVC(gamma=0.001)

train_sizes, train_loss, test_loss = learning_curve(model, X, y, cv=10, scoring='neg_mean_squared_error', train_sizes=[0.1, 0.25, 0.5, 0.75, 1])
# 平均每一轮所得到的平均方差(共5轮，分别为样本10%、25%、50%、75%、100%)
train_loss_mean = -np.mean(train_loss, axis=1)
test_loss_mean = -np.mean(test_loss, axis=1)

# 可视化图形
import matplotlib.pyplot as plt
plt.plot(train_sizes, train_loss_mean, label="Train")
plt.plot(train_sizes, test_loss_mean, label="Test")
plt.legend()
plt.show()

如果我们把上面代码中SVC参数的gamma值设置为0.1，显示出的图形为：

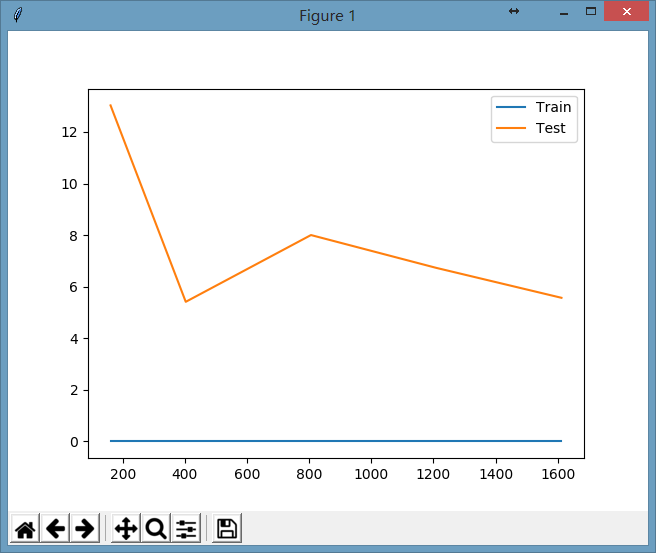
在上面的图形中，我们会发现再增加训练集的数据并没有使测试集的损失值下降，相当于一个人按照他的学习方式做训练题已经够多了，你做更多的训练题都无法提高你的考试成绩了，这时可能需要考虑的是稍微改变一下你的学习方法说不定就能提高考试成绩呢。

这也说明了，在某些情况下题海战术不一定奏效了。

在机器学习中表示为所学到的模型可能太复杂了，产生了过拟合（过拟合表现为训练集的损失函数在下降，但测试集的损失函数不降反升），不具备泛化能力，例如下图中绿色曲线就是一个过拟合的表现：

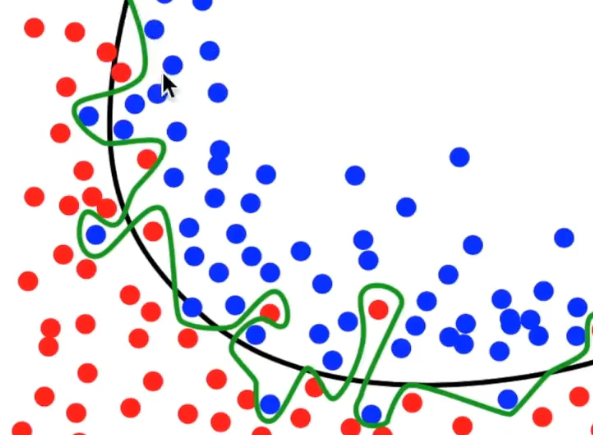
相应的损失函数曲线显示如下所示：

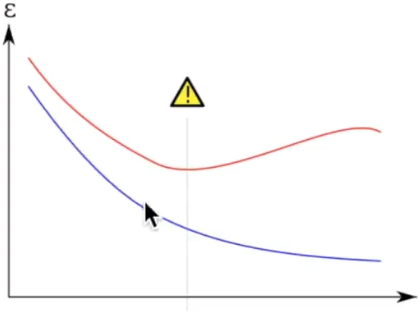
因此如果我们想要查看是否有过拟合，可以通过learning_curve函数来进行并以可视化的方式来查看结果。