第四十一课 KMP子串查找算法

问题：

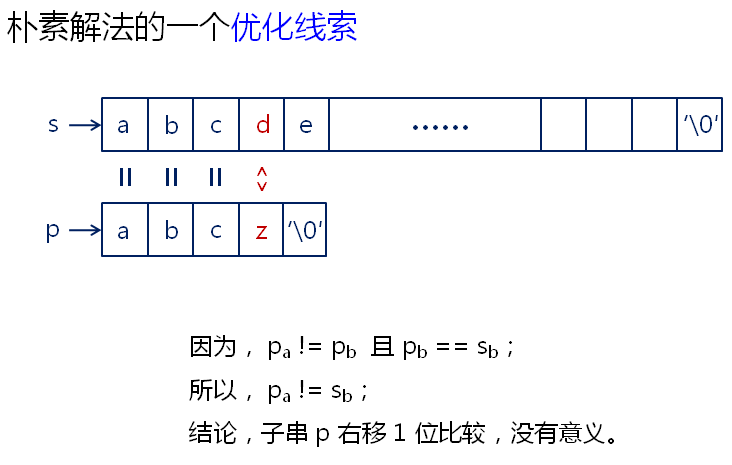
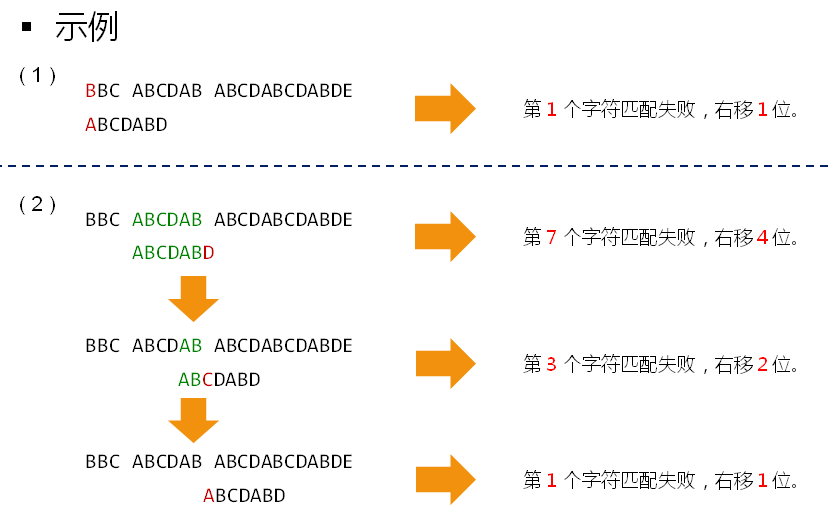
右移的位数和目标串没有多大的关系，和子串有关系。

已匹配的字符数现在已经有了，部分匹配值还没有。

前六位匹配成功就去查找PMT中的第六位。

现在的任务就是求得部分匹配表。

问题：怎么得到部分匹配表呢？

前缀集合和后缀集合取最长的交集就是部分匹配值。

例如，上图中前缀和后缀没有交集，部分匹配值就是0。

问题：

怎么编程产生部分匹配表呢？

从第2个字符开始递推，做一个贪心的假设，我们现在要求的匹配值是由上一次得到的匹配值加1得到。

假设有5个字符，当前的匹配值是3，当有6个字符时，我们就假设匹配值是4。

推导过程：

ll值定义为前缀和后缀交集元素的最大长度。

第一个元素的ll值为0。

当前要求的ll是以历史的ll值求出来的。

当可选的ll值为0时，直接比对首尾元素，若不相等则为0，若相等则为1。

例如：

ab的ll值为0，当向后扩展一个字符求aba的ll值时，需要根据ab的ll值来求，

　　因为ab的ll值为0，我们只需要比对aba中的第一个a和最后一个a，发现相等，于是aba的ll值为1。

再向后扩展一个字符abab，这时候上一个ll值不为零，我们就以上次匹配的字符a为种子，向后扩展比较，第一个a向后扩展一下为ab，

　　第三个a向后扩展一下为ab，a和a比较相等（这个已经比对过），b和b比较相等，于是abab的ll值为1+1=2。

再向后扩展一个字符ababa，上一个ll值不为0，我们以ab为种子，分别向后扩展一个字符，得到aba（前三个）和aba（后三个），

　　ab和ab已经比对过了，于是只需要比对最后一个a和a，发现相等，于是ll值为2+1=3。

再向后扩展一个字符ababax，上一个ll值不为0，现在分别以aba为种子向后扩展一个字符，得到abab（前四个）和abax（后四个），

　　aba和aba刚才已经比对过，现在比较b和x发现不相等，于是，为了还能扩展，我们需要在abc中找一个种子继续扩展看一下，

　　如上图中两个画红圈的a，这就是aba的前缀和aba的后缀的最大交集，这两个aba是方框中的aba，一个是aba(1-3)，一个是aba(3-5)。

　　于是，我们需要aba的最大匹配值，我们去查找aba这个字符串的最大匹配值，这个刚才已经求得了，

　　查PMT[3]即可，aba的ll值为1，于是以第一个a和第五个a为种子，分别向后扩展一个字符，得到ab和ax，a和a已经比对过，

　　现在比较b和x发现不相等，于是再去查a这个字符串的匹配值，我们也已经求出来了是0，因为a的ll值为0，所以我们直接比对首尾

　　元素，于是比较第一个a和最后一个元素x，发现不相等，于是ababax的ll值为0。

上面abab和abax匹配不上时，我们直接查找的PMT[3]，而略过了PMT[2]，这是为什么呢？

假设可选的ll值为2，这时前缀就是ab，后缀就是ba，然后以这里的前后缀作为种子来扩展，这时可以看出，不用扩展就可以知道，

肯定不会匹配，因为ab和ba就匹配不上，为什么ll值为2就是不对呢？

因为要使得有相同的前缀和后缀进行扩展，必然的要去前缀和后缀元素的交集的最大长度，aba和aba前缀、后缀交集的最大长度就是aba的ll值，因此，只能拿a来进行扩展。

编程实现：

 #include <iostream>
 #include <cstring>
 #include "DTString.h"

 using namespace std;
 using namespace DTLib;

 int* make_pmt(const char* p)
 {
     int len = strlen(p);

     int* ret = static_cast<int*>(malloc(sizeof(int) * len));

     if( ret != NULL )
     {
         int ll = ;

         ret[] = ; // 第0个元素（长度为1的字符串）的ll值为0

         for(int i = ; i < len; i++)
         {
             //不成功的情况
             while( (ll > ) && (p[ll] != p[i]) )
             {
                 ll = ret[ll];
             }

             // 假设最理想的情况成立
             //在前一个ll值的基础行进行扩展，只需比对最后扩展的字符是否相等
             //相等的话ll值加1，并写入到部分匹配表
             if( p[ll] == p[i] )
             {
                 ll++;
             }

             ret[i] = ll; // 将ll值写入匹配表

         }
     }

     return ret;
 }

 int main()
 {
     int* pmt = make_pmt("ababax");

     for(int i = ; i < strlen("ababax"); i++)
     {
         cout << i << ":" << pmt[i] << endl;
     }

     return ;
 }

结果如下：

测试程序2：

 #include <iostream>
 #include <cstring>
 #include "DTString.h"

 using namespace std;
 using namespace DTLib;

 int* make_pmt(const char* p)
 {
     int len = strlen(p);

     int* ret = static_cast<int*>(malloc(sizeof(int) * len));

     if( ret != NULL )
     {
         int ll = ;

         ret[] = ; // 第0个元素（长度为1的字符串）的ll值为0

         for(int i = ; i < len; i++)
         {
             //不成功的情况
             while( (ll > ) && (p[ll] != p[i]) )
             {
                 ll = ret[ll];
             }

             // 假设最理想的情况成立
             //在前一个ll值的基础行进行扩展，只需比对最后扩展的字符是否相等
             //相等的话ll值加1，并写入到部分匹配表
             if( p[ll] == p[i] )
             {
                 ll++;
             }

             ret[i] = ll; // 将ll值写入匹配表

         }
     }

     return ret;
 }

 int main()
 {
     int* pmt = make_pmt("ABCDABD");

     for(int i = ; i < strlen("ABCDABD"); i++)
     {
         cout << i << ":" << pmt[i] << endl;
     }

     return ;
 }

结果如下：

KMP子串查找算法：

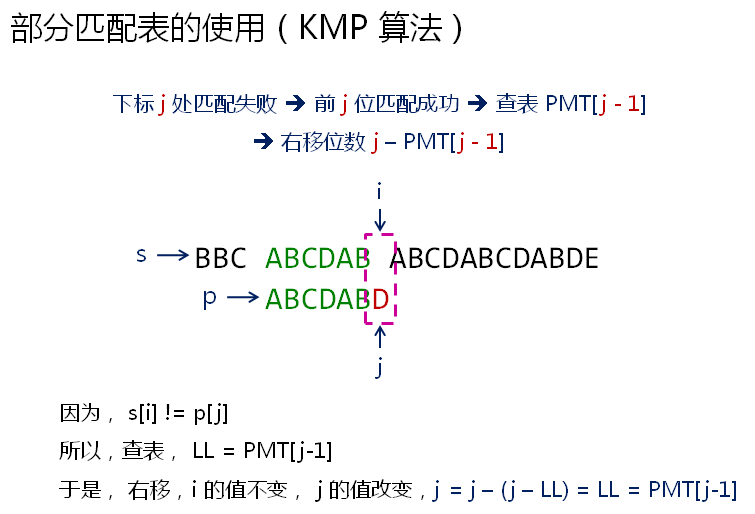
j为6时不匹配，前j位匹配成功，查PMT[j-1]，得出右移位数 j - PMT[j - 1]，也就是 j - LL，子串ABCDABD右移 j - LL位之后，j的值就变为 j - (j - LL)，即LL。

程序如下：

 #include <iostream>
 #include <cstring>
 #include "DTString.h"

 using namespace std;
 using namespace DTLib;

 int* make_pmt(const char* p)  // O(m)
 {
     int len = strlen(p);

     int* ret = static_cast<int*>(malloc(sizeof(int) * len));

     if( ret != NULL )
     {
         int ll = ;

         ret[] = ; // 第0个元素（长度为1的字符串）的ll值为0

         for(int i = ; i < len; i++)
         {
             //不成功的情况
             while( (ll > ) && (p[ll] != p[i]) )
             {
                 ll = ret[ll];
             }

             // 假设最理想的情况成立
             //在前一个ll值的基础行进行扩展，只需比对最后扩展的字符是否相等
             //相等的话ll值加1，并写入到部分匹配表
             if( p[ll] == p[i] )
             {
                 ll++;
             }

             ret[i] = ll; // 将ll值写入匹配表

         }
     }

     return ret;
 }

 int kmp(const char* s, const char* p)  //O(m) + O(n) = O(m + n)
 {
     int ret = -;

     int sl = strlen(s);
     int pl = strlen(p); //子串

     int* pmt = make_pmt(p);   //O(m)

     if( (pmt != NULL) && ( < pl) && (pl <= sl))
     {
         for( int i = ,j = ; i < sl; i++ )
         {
             while( (j > ) && (s[i] != p[j]) ) // j小于等于0时要退出
             {
                 j = pmt[j];
             }

             if( s[i] == p[j] )
             {
                 j++;
             }

             if( j == pl ) // j的值如果最后就是子串的长度，意味着查找到了
             {
                 ret = i +  - pl; // 匹配成功时i的值停在最后一个匹配的字符上
                 break;
             }
         }
     }

     free(pmt);

     return ret;
 }

 int main()
 {
     cout << kmp("abcde", "cde") << endl;
     cout << kmp("ababax", "ba") << endl;
     cout << kmp("ababax", "ax") << endl;
     cout << kmp("ababax", "") << endl;
     cout << kmp("ababax", "ababax") << endl;
     cout << kmp("ababax", "ababaxy") << endl;

     return ;
 }

KMP具有线性时间复杂度，最朴素的算法的时间复杂度是O(m*n)。

第69行的计算图解如下：

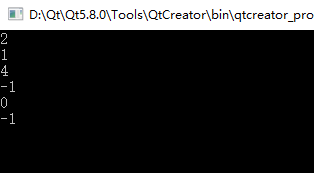
程序运行结果如下：

小结：