SoapUI中的RegEx
在for Content matching RegEx中
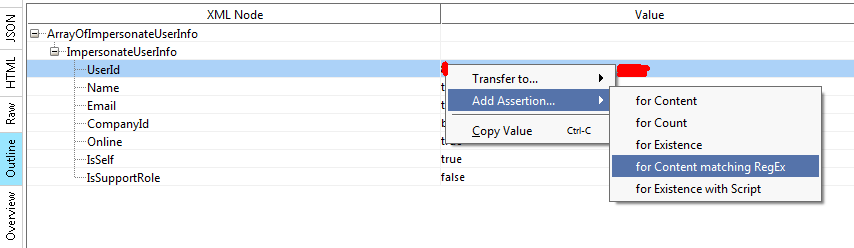
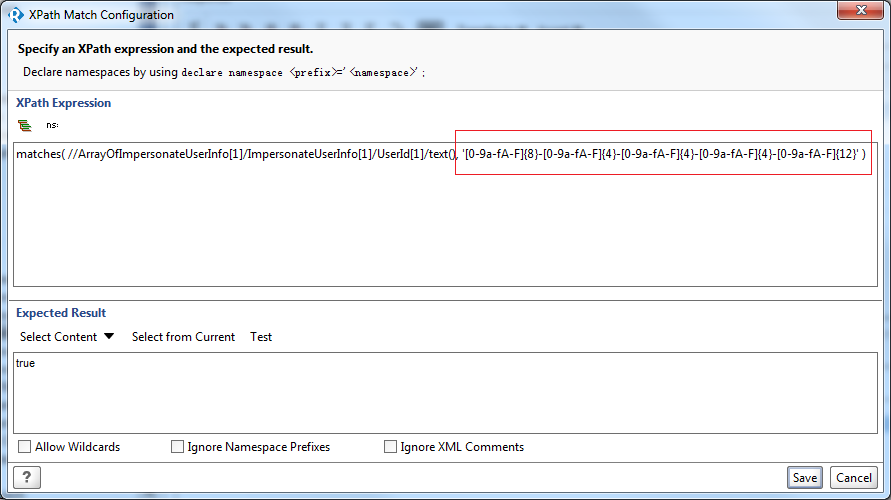
SoapUI中的RegEx的更多相关文章
- 使用Groovy处理SoapUI中Json response
最近工作中,处理最多的就是xml和json类型response,在SoapUI中request里面直接添加assertion处理json response的话,可以采用以下方式: import gro ...
- 在SoapUI中模拟用户操作
SoapUI作为一款接口测试工具,具有极大的灵活性和拓展性.它可以通过安装插件,拓展其功能.Selenium作为一款Web自动化测试插件可以很好的与SoapUI进行集成.如果要在SoapUI中模拟用户 ...
- excel文件的groovy脚本在SoapUI中进行数据驱动测试
SoapUI Pro具有从外部文件读取数据的功能,例如:excel,csv等.但SoapUI不提供从excel文件读取数据的功能.因此,为了从SoapUI中的excel文件中读取数据,我们需要在gro ...
- SoapUI中Groovy的实用方法
1.依照上次结果判断下步是否执行: import com.eviware.soapui.model.testsuite.TestStepResult.TestStepStatus myTestStep ...
- SoapUI中读取法文字符
最近测试中,使用SoapUI时需要读取excel中的法文数据作为参数,groovy script中使用的是jxl进行excel的读取, 开始时一直显示乱码,而后在script中添加如下wookbook ...
- java中split(regex)使用中要注意的问题:正则表达式
比如我在项目中遇到的(,),.,|,*等等类的符号: String area="(30.13206313822174, 120.4156494140625)(29.8763738070713 ...
- R中的Regex
Description grep.grepl.regexpr.gregexpr和regexec在字符向量的每个元素中搜索与参数模式匹配的参数:它们在结果的格式和详细程度上有所不同. sub和gsub分 ...
- SoapUI中如何传递cookie
import com.eviware.soapui.support.types.StringToStringMap //Get all the cookies in the response def ...
- SoapUI中XML解析
From http://www.robert-nemet.com/2011/11/groovy-xml-parsing-in-soapui.html Introduction Since soapUI ...
随机推荐
- 「 Luogu P2196 」 挖地雷
# 解题思路 跑 $\text{n}$ 遍 $\text{spfa}$ 并记录路径,找到比当前最长路长的就更新答案,并且将路径也更新,注意起点的处理. # 附上代码 #include <iost ...
- HashMap、ConcurrentHashMap以及HashTable(面试向)
---->HashMap 在java1.7中,hashmap的数据结构是基于数组+链表的结构,即我们比较熟悉的Entry数组,其包含的(key-value)键值对的形式.在多线程环境下,Hash ...
- [Python3网络爬虫开发实战] 2.5-代理的基本原理
我们在做爬虫的过程中经常会遇到这样的情况,最初爬虫正常运行,正常抓取数据,一切看起来都是那么美好,然而一杯茶的功夫可能就会出现错误,比如403 Forbidden,这时候打开网页一看,可能会看到“您的 ...
- Linux命令整理(2018/9/9-2018/9/15)
根据本周的Linux学习进度,整理了部分Linux知识及常用命令,待完善…… 1.显示默认启动方式(默认启动目标): systemctl get-default 2.设置默认启动方式(默认启动目标): ...
- First C program
come from https://mooc.study.163.com/learn/1000002011?tid=2001530003#/learn/content?type=detail& ...
- SPOJ 3261 (树套树傻逼题)
As another one of their crazy antics, the N (1 ≤ N ≤ 100,000) cows want Farmer John to race against ...
- [NOIP2005] 普及组 循环
陶陶摘苹果 校门外的树 采药 以上三道都不是重点 循环 题目描述 乐乐是一个聪明而又勤奋好学的孩子.他总喜欢探求事物的规律.一天,他突然对数的正整数次幂产生了兴趣. 众所周知,2的正整数次幂最后一位数 ...
- 【BZOJ3110】K大数查询(权值线段树套线段树+标记永久化,整体二分)
题意:有N个位置,M个操作.操作有两种,每次操作 如果是1 a b c的形式表示在第a个位置到第b个位置,每个位置加入一个数c 如果是2 a b c形式,表示询问从第a个位置到第b个位置,第C大的数是 ...
- Mutual Training for Wannafly Union #9
A(SPOJ NPC2016A) 题意:给一个正方形和内部一个点,要求从这个点向四边反射形成的路线的长度 分析:不断做对称,最后等价于求两个点之间的距离 B(CF480E) 题意:求01矩阵内由0组成 ...
- codeforces 762E(cdq分治)
题意: n个电台,每个电台有三个属性xi, ri, fi.分别代表电台的坐标,电台的播报范围,以及播报的频率. 对于一对电台i, j,若min(ri, rj) >= |xi - xj|,那么他们 ...
