UVALive 6811 Irrigation Line(二分图最小点覆盖--匈牙利算法)

题意：求最少的线可以覆盖一个由0、1两种数字组成的图中所有的1。

eg：

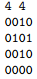只需要两条线即可。

分析：

1、先为上述例子的行列标号

2、若图中数字为1，则代表该数字所在的行与列有关联。

例如第r1行第c3列的数字1，可以看成r1和c3为两个点，因为此处是数字1，所以这两个点之间可以连1条线

3、所以可转化为如下的二分图

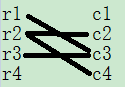
4、可以简单的理解为只要图中某个位置是数字1，就可以连一条线，线的两个端点是行号和列号。

5、因此本题就转化为了，求能覆盖所有边的最少的点数

6、由上图易知，r2和c3两个点就可以覆盖所有的边，回到原题就是只要在第r2行和第c3列画上线即可覆盖所有的1

7、由二分图的性质可知，最小匹配数等于最大点覆盖数，因此用匈牙利算法求解。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define Min(a, b) a < b ? a : b
#define Max(a, b) a < b ? b : a
typedef long long ll;
typedef unsigned long long llu;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const ll LL_INF = 0x3f3f3f3f3f3f3f3f;
const ll LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {, , -, };
const int dc[] = {-, , , };
const double pi = acos(-1.0);
const double eps = 1e-;
const int MAXN =  + ;
const int MAXT =  + ;
using namespace std;
char a[MAXN][MAXN];
int mp[MAXN][MAXN];
int match[MAXN];
bool used[MAXN];
int M, N;
bool Find(int x){
    for(int i = ; i <= N; ++i){
        if(!used[i] && mp[x][i]){
            used[i] = true;
            if(!match[i] || Find(match[i])){
                match[i] = x;
                return true;
            }
        }
    }
    return false;
}
void solve(){
    int ans = ;
    for(int i = ; i <= M; ++i){
        memset(used, false, sizeof used);
        if(Find(i)) ++ans;
    }
    printf("%d\n", ans);
}
int main(){
    int T;
    scanf("%d", &T);
    for(int i = ; i <= T; ++i){
        memset(a, , sizeof a);
        memset(mp, , sizeof mp);
        memset(match, , sizeof match);
        scanf("%d%d", &M, &N);
        for(int i = ; i < M; ++i){
            scanf("%s", a[i]);
        }
        for(int i = ; i < M; ++i){
            for(int j = ; j < N; ++j){
                if(a[i][j] == ''){
                    mp[i + ][j + ] = ;
                }
            }
        }
        printf("Case #%d: ", i);
        solve();
    }
    return ;
}