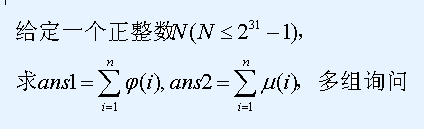2019.02.12 bzoj3944: Sum(杜教筛)
传送门
题意:
思路:直接上杜教筛。
知道怎么推导就很简单了,注意预处理的范围。
然后我因为预处理范围不对被zxyoi教育了(ldx你这个傻×两倍常数活该被卡TLE) 喜闻乐见
代码:
#include<bits/stdc++.h>
#define ri register int
using namespace std;
const int N=7500005,lim=7500000;
typedef long long ll;
namespace Sieve{
int pri[N],tot=0,mu[N];
ll phi[N];
bool vis[N];
map<int,int>mpa;
map<int,ll>mpb;
inline void init(){
vis[1]=phi[1]=mu[1]=1;
for(ri i=2;i<=lim;++i){
if(!vis[i])pri[++tot]=i,phi[i]=i-1,mu[i]=-1;
for(ri j=1;j<=tot&&i*pri[j]<=lim;++j){
vis[i*pri[j]]=1;
if(i==i/pri[j]*pri[j]){
phi[i*pri[j]]=pri[j]*phi[i],mu[i*pri[j]]=0;
break;
}
phi[i*pri[j]]=(pri[j]-1)*phi[i],mu[i*pri[j]]=-mu[i];
}
}
for(ri i=2;i<=lim;++i)phi[i]+=phi[i-1],mu[i]+=mu[i-1];
}
inline int Mu(const int&x){
if(x<=lim)return mu[x];
if(mpa[x])return mpa[x];
int ret=0;
for(ri l=2,r;r<x&&l<=x;l=r+1)r=x/(x/l),ret+=Mu(x/l)*(r-l+1);
return mpa[x]=1-ret;
}
inline ll Phi(const int&x){
if(x<=lim)return phi[x];
if(mpb[x])return mpb[x];
ll ret=0;
for(ri l=2,r;r<x&&l<=x;l=r+1)r=x/(x/l),ret+=Phi(x/l)*(r-l+1);
return mpb[x]=(ll)x*((ll)x+1)/2-ret;
}
}
int main(){
freopen("lx.in","r",stdin);
Sieve::init();
int tt,n;
scanf("%d",&tt);
while(tt--)scanf("%d",&n),cout<<Sieve::Phi(n)<<' '<<Sieve::Mu(n)<<'\n';
return 0;
}
2019.02.12 bzoj3944: Sum(杜教筛)的更多相关文章
- [BZOJ3944]Sum(杜教筛)
3944: Sum Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 6201 Solved: 1606[Submit][Status][Discuss ...
- [bzoj3944] sum [杜教筛模板]
题面: 传送门 就是让你求$ \varphi\left(i\right) $以及$ \mu\left(i\right) $的前缀和 思路: 就是杜教筛的模板 我们把套路公式拿出来: $ g\left( ...
- bzoj3944: Sum 杜教筛板子题
板子题(卡常) 也可能是用map太慢了 /************************************************************** Problem: 3944 Us ...
- 3944: Sum[杜教筛]
3944: Sum Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 3471 Solved: 946[Submit][Status][Discuss] ...
- 【Bzoj3944】杜教筛模板(狄利克雷卷积搞杜教筛)
题目链接 哇杜教筛超炫的 有没有见过$O(n^\frac{2}{3})$求欧拉函数前缀和的算法?没有吧?蛤蛤蛤 首先我们来看狄利克雷卷积是什么 首先我们把定义域是整数,陪域是复数的函数叫做数论函数. ...
- HDU6706 huntian oy(2019年CCPC网络赛+杜教筛)
目录 题目链接 思路 代码 题目链接 传送门 思路 看到这题还比较懵逼,然后机房大佬板子里面刚好有这个公式\(gcd(a^n-b^n,a^m-b^m)=a^{gcd(n,m)}-b^{gcd(n,m) ...
- 洛谷P4213 Sum(杜教筛)
题目描述 给定一个正整数N(N\le2^{31}-1)N(N≤231−1) 求ans_1=\sum_{i=1}^n\phi(i),ans_2=\sum_{i=1}^n \mu(i)ans1=∑i=1 ...
- bzoj 3944 Sum —— 杜教筛
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=3944 杜教筛入门题! 看博客:https://www.cnblogs.com/zjp-sha ...
- BZOJ 3944: Sum [杜教筛]
3944: Sum 贴模板 总结见学习笔记(现在还没写23333) #include <iostream> #include <cstdio> #include <cst ...
随机推荐
- 20165312 2017-2018-2 《JAVA程序设计》第2周学习总结
20165312 2017-2018-2 <JAVA程序设计>第2周学习总结 一.对上一周学习的查漏补缺 1.上周在虚拟机中进行编译程序时出现错误,在上一周的博客中我有提到,当时还未找到解 ...
- SQLServer、MySQL、Oracle如何查看所有表的条数
SQLServer: create table #t(name varchar(255), rows bigint, reserved varchar(20), data varchar(20), i ...
- vs与linux的交叉编译环境搭建
很久之前就想写一个linux服务器,但是对linux的vim编译工具又不是很熟,只能在win环境下写好代码拷贝到linux环境下编译运行,现在VS出了一个插件可以对linux代码远程在linux环境下 ...
- hive的使用
1,前言 书接上回,接着对上一个hive安装后环境下的hive使用.
- Servlet】(2)有关Servlet实现的几个类:GenericServlet、HttpServlet、ServletConfig、ServletContext
一.GenericServlet 1.所有的成员方法: 1.在javaWeb项目中: 2.web.xml <?xml version="1.0" encoding=" ...
- android toolbar使用记录
1.打开Project structure,选择app modules,切换到Dependencies添加com.android.support.design.26.0.0.alpha1 2.在lay ...
- Rabbitmq(6) 主题模式
* 匹配1个 # 匹配所有 发送者: package com.aynu.bootamqp.service; import com.aynu.bootamqp.commons.utils.Amqp; i ...
- 异步请求Ajax(取得json数据)
异步请求Ajax 没有学习Ajax之前请求数据的时候都是整个页面全部刷新了一次,也就是每次请求都会重新请求所有的资源.但是在很多时候不需要页面全部刷新,仅仅是需要页面的局部数据刷新即可,此时需要发送异 ...
- SQL 中的语法顺序与执行顺序
FROM : HOME SQL 是一种声明式语言 SQL 语言是为计算机声明了一个你想从原始数据中获得什么样的结果的一个范例,而不是告诉计算机如何能够得到结果. SQL 语言声明的是结果集的属性,计算 ...
- Maven项目中遇到的问题及其解决方案
Maven中pom报红 1.jdk版本是否符合要求? 2.maven的本地confg中的setting.xml中是否和要求的jdk版本一致? 3.maven本地仓库路径是否正确,即为自己的确定的仓库位 ...