JavaScript图形实例:Koch曲线
Koch曲线的构造过程是:取一条长度为L0的直线段,将其三等分,保留两端的线段,将中间的一段改换成夹角为60度的两个等长直线;再将长度为L0/3的4个直线段分别进行三等分,并将它们中间的一段均改换成夹角为60度的两段长为L0/9的直线段;重复以上操作直至无穷,可得以一条具有自相似结构的折线,如图1所示。
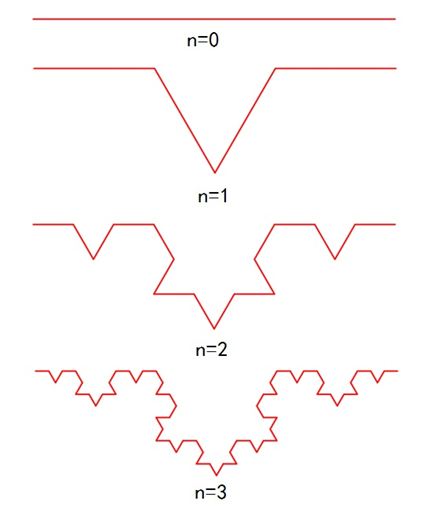
图1 Koch曲线的生成
Koch曲线采用递归过程易于实现,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>Koch曲线</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="400" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var maxdepth =5;
var curdepth = 0;
ctx.lineWidth = 2;
Koch({x:50,y:150},{x:550,y:150},Math.PI/3);
function Koch(p1,p2,angle)
{
curdepth++;
if (curdepth<=maxdepth)
{
var x1=(2*p1.x+p2.x)/3;
var y1=(2*p1.y+p2.y)/3;
var x3=(2*p2.x+p1.x)/3;
var y3=(2*p2.y+p1.y)/3;
var x2=(x3-x1)*Math.cos(angle)-(y3-y1)*Math.sin(angle)+x1;
var y2=(x3-x1)*Math.sin(angle)+(y3-y1)*Math.cos(angle)+y1;
Koch(p1,{x:x1,y:y1},Math.PI/3);
Koch({x:x1,y:y1},{x:x2,y:y2},Math.PI/3);
Koch({x:x2,y:y2},{x:x3,y:y3},Math.PI/3);
Koch({x:x3,y:y3},p2,Math.PI/3);
}
if (curdepth>maxdepth)
draw([p1,{x:x1,y:y1},{x:x2,y:y2},{x:x3,y:y3},p2]);
curdepth--;
}
function draw(points)
{
ctx.strokeStyle = "red";
ctx.beginPath()
ctx.moveTo(points[0].x,points[0].y)
for(i=1;i<points.length;i++)
{
ctx.lineTo(points[i].x,points[i].y);
}
ctx.closePath()
ctx.stroke()
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的Koch曲线,如图2所示。

图2 递归深度maxdepth =5的Koch曲线
由图1和2可知,Koch曲线的初始图元是直线,但最终结果却是一条参差不齐的曲线,很像雪花的边缘,如果将3条这样的曲线围在一起,便得到Koch雪花的图案。这样,初始图元不是一条直线,而是一个等边三角形。Koch雪花的生成示例如图3所示。

图3 Koch雪花的生成
在程序设计时,定义好等边三角形的三个顶点坐标,调用三次Koch递归过程,以实现等边三角形三条边各自的Koch曲线生成,即可得到Koch雪花图案。编写的HTML文件如下。
<!DOCTYPE html>
<head>
<title>Koch雪花</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById('myCanvas');
var ctx = canvas.getContext('2d');
var maxdepth =5;
var curdepth = 0;
ctx.lineWidth = 2;
Koch({x:50,y:450},{x:500,y:450},Math.PI/3);
Koch({x:275,y:450-225*Math.sqrt(3)},{x:50,y:450},Math.PI/3);
Koch({x:500,y:450},{x:275,y:450-225*Math.sqrt(3)},Math.PI/3);
function Koch(p1,p2,angle)
{
curdepth++;
if (curdepth<=maxdepth)
{
var x1=(2*p1.x+p2.x)/3;
var y1=(2*p1.y+p2.y)/3;
var x3=(2*p2.x+p1.x)/3;
var y3=(2*p2.y+p1.y)/3;
var x2=(x3-x1)*Math.cos(angle)-(y3-y1)*Math.sin(angle)+x1;
var y2=(x3-x1)*Math.sin(angle)+(y3-y1)*Math.cos(angle)+y1;
Koch(p1,{x:x1,y:y1},Math.PI/3);
Koch({x:x1,y:y1},{x:x2,y:y2},Math.PI/3);
Koch({x:x2,y:y2},{x:x3,y:y3},Math.PI/3);
Koch({x:x3,y:y3},p2,Math.PI/3);
}
if (curdepth>maxdepth)
draw([p1,{x:x1,y:y1},{x:x2,y:y2},{x:x3,y:y3},p2]);
curdepth--;
}
function draw(points)
{
ctx.strokeStyle = "red";
ctx.beginPath()
ctx.moveTo(points[0].x,points[0].y)
for(i=1;i<points.length;i++)
{
ctx.lineTo(points[i].x,points[i].y);
}
ctx.closePath()
ctx.stroke()
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,在浏览器窗口中可能会绘制出如图4所示的Koch雪花图案。

图4 递归深度maxdepth =5的Koch雪花图案
JavaScript图形实例:Koch曲线的更多相关文章
- JavaScript图形实例:线段构图
在“JavaScript图形实例:四瓣花型图案”和“JavaScript图形实例:蝴蝶结图案”中,我们绘制图形时,主要采用的方法是先根据给定的曲线参数方程计算出两点坐标,然后将两点用线段连接起来,线段 ...
- JavaScript动画实例:曲线的绘制
在“JavaScript图形实例:曲线方程”一文中,我们给出了15个曲线方程绘制图形的实例.这些曲线都是根据其曲线方程,在[0,2π]区间取一系列角度值,根据给定角度值计算对应的各点坐标,然后在计算出 ...
- JavaScript图形实例:再谈IFS生成图形
在“JavaScript图形实例:迭代函数系统生成图形”一文中,我们介绍了采用迭代函数系统(Iterated Function System,IFS)创建分形图案的一些实例.在该文中,仿射变换函数W的 ...
- JavaScript图形实例:随机SierPinski三角形
在“JavaScript图形实例:SierPinski三角形”中,我们介绍了SierPinski三角形的基本绘制方法,在“JavaScript图形实例:迭代函数系统生成图形”一文中,介绍了采用IFS方 ...
- JavaScript图形实例:Hilbert曲线
德国数学家David Hilbert在1891年构造了一种曲线,首先把一个正方形等分成四个小正方形,依次从西北角的正方形中心出发往南到西南正方形中心,再往东到东南角的正方形中心,再往北到东北角正方形中 ...
- JavaScript图形实例:四瓣花型图案
设有坐标计算公式如下: X=L*(1+SIN(4α))*COS(α) Y=L*(1+SIN(4α))*SIN(α) 用循环依次取α值为0~2π,计算出X和Y,在canvas画布中对坐标位置(X,Y)描 ...
- JavaScript图形实例:图形的旋转变换
旋转变换:图形上的各点绕一固定点沿圆周路径作转动称为旋转变换.可用旋转角表示旋转量的大小. 旋转变换通常约定以逆时针方向为正方向.最简单的旋转变换是以坐标原点(0,0)为旋转中心,这时,平面上一点P( ...
- JavaScript图形实例:圆内螺线
数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词来源于希腊文,它的原意是“旋卷”或“缠卷”.例如,平面螺旋线便是以一个固定点开始向外逐圈旋绕而形成的曲线. 阿基米德螺线和黄 ...
- JavaScript图形实例:正多边形
圆心位于坐标原点,半径为R的圆的参数方程为 X=R*COS(θ) Y=R*SIN(θ) 在圆上取N个等分点,将这N个点首尾连接N条边,可以得到一个正N边形. 1.正多边形阵列 构造一个8行8列的正N( ...
随机推荐
- Java实现 蓝桥杯VIP 算法训练 会议中心
算法训练 会议中心 时间限制:2.0s 内存限制:512.0MB 会议中心 Siruseri政府建造了一座新的会议中心.许多公司对租借会议中心的会堂很感兴趣,他们希望能够在里面举行会议. 对于一个客户 ...
- SQL Server账号密码(sa)登录失败 错误原因:233
(其实以前经常用的时候,都很简单,最近一段时间不用了,再一看发现都忘记的差不多了,还是写一篇博客吧,防止下一次再在这种问题上面浪费时间) 右键此电脑,点击管理 如果没有此电脑打开文件夹 在这里右键也是 ...
- Java实现 洛谷 P1200 [USACO1.1]你的飞碟在这儿Your Ride Is He…
import java.util.Scanner; public class Main{ private static Scanner cin; public static void main(Str ...
- Linux文件搜索命令locate、which、grep详解
命令locate详解 命令locate,其基本功能是在文件资料库中可以快速的搜索系统文件,占用系统资源很少,例如:locate my.cnf 还可以使用locate -i [文件名],不区分大小写进行 ...
- 小师妹学JavaIO之:目录还是文件
目录 简介 linux中的文件和目录 目录的基本操作 目录的进阶操作 目录的腰疼操作 总结 简介 目录和文件傻傻分不清楚,目录和文件的本质到底是什么?在java中怎么操纵目录,怎么遍历目录.本文F师兄 ...
- 滴滴数据驱动利器:AB实验之分组提效
桔妹导读:在各大互联网公司都提倡数据驱动的今天,AB实验是我们进行决策分析的一个重要利器.一次实验过程会包含多个环节,今天主要给大家分享滴滴实验平台在分组环节推出的一种提升分组均匀性的新方法.本文首先 ...
- 如何通过IAM打造零信任安全架构
万物互联时代来临,面对越来越严峻的企业网络安全及复杂的(如微服务,容器编排和云计算)开发.生产环境,企业 IT 急需一套全新的身份和访问控制管理方案. 为了满足企业需求,更好的服务企业用户,青云Qin ...
- Error reporting for dbus
D-Bus 1.13.14 目录 Detailed Description Function Documentation ◆ dbus_error_free() ◆ dbus_error_has_na ...
- <VCC笔记> 推断操作符,映射和量词
推断操作符 在VCC中,==>符号意味着逻辑推理结果,即离散数学中的蕴涵关系.P==>Q等价于((!P)||(Q)).是非常常用的操作符. 量词(quantifier) 关于量词,这里指的 ...
- CSS文本相关之水平排列[4]
在正常流中,文本都是从左往右.自上而下排列显示,如果想要改变排列方向的话,可以通过CSS属性来改变. text-align属性 文本排列(text-align)可改变文本在水平上的方向,但不改变内部的 ...
