波动数列 神奇的dp

问题描述

　　观察这个数列：
　　1 3 0 2 -1 1 -2 ...

　　这个数列中后一项总是比前一项增加2或者减少3。

　　栋栋对这种数列很好奇，他想知道长度为 n 和为 s 而且后一项总是比前一项增加a或者减少b的整数数列可能有多少种呢？

输入格式

　　输入的第一行包含四个整数 n s a b，含义如前面说述。

输出格式

　　输出一行，包含一个整数，表示满足条件的方案数。由于这个数很大，请输出方案数除以100000007的余数。

样例输入

4 10 2 3

样例输出

2

样例说明

　　这两个数列分别是2 4 1 3和7 4 1 -2。

数据规模和约定

　　对于10%的数据，1<=n<=5，0<=s<=5，1<=a,b<=5；
　　对于30%的数据，1<=n<=30，0<=s<=30，1<=a,b<=30；
　　对于50%的数据，1<=n<=50，0<=s<=50，1<=a,b<=50；
　　对于70%的数据，1<=n<=100，0<=s<=500，1<=a, b<=50；
　　对于100%的数据，1<=n<=1000，-1,000,000,000<=s<=1,000,000,000，1<=a, b<=1,000,000。

--------------------------------------------------------------------------------------------------------------------------

我算是摸透了，蓝桥杯最后两题如果数据大，肯定不是dfs，多半是DP

这个题是如何变出一个DP的递推公式呢，贼神奇

把a,b归结为一个状态p，第i个数要么是加a，要么是加b

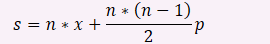
对于n个数而言，a和b的总次数是 从1累加到(n-1)

我们暂且不论x是什么数，我们研究的是a出现的次数

对于第i个数来说 要么是a出现，要么是a不出现b出现，这两种状态

网上的思路大概是这样，dp[i-1][j]表示的是第i个数不取a

我想了很久，为什么dp[i-1][j-i]是表示第i个数取a，其他人对j有两种解释

1. dp（i，j）表示序列的前 i 项中 a 的次数为 j 时的方案种数。

2.dp[i][j]，表示前i个元素组成和为j的序列的方案数，这里的和j表示的是所有的a的和.

但是j的范围是

我是这么理解的 i表示前i项，而j是a出现次数的和，不是a一共出现了多少次，而是从1累加到出现的次数。

比如对于前两项而言，a只能出现1次或者2次，那么j的最大值就是1+2 = 3

　　对于前三项而言，a只能出现1，2，3次，那么j的最大值就是1+2+3 = 6

我之前在这里想了好久好久，抱住萌萌的自己。

dp[0][0] = 1

dp[1][0] = dp[0][0] = 1 || dp[1][1] = dp[0][1]+dp[0][0] = 1

dp[2][0] = dp[1][0] = 1 || dp[2][1] = dp[1][1] =1 || dp[2][2] = dp[1][2] + dp[1][0] = 1 || dp[2][3] = dp[1][3] + dp[1][1] = 1

dp用滚动数组节省空间，最后判断x是不是整数。

 #include<iostream>
 using namespace std;
 #define MOD 100000007
 #define MAXN 1100
 long long  n,s,a,b;
 long long all;
 long long Bo[2][MAXN*MAXN];//作为滚动数组
 int p=0;
 //p为滚动数组标识，表示当前操作数组的第几行，（例如当前计算第i行，p指向操作Bo数组第0行，逻辑上i-1行是Bo数组第1行）
 void fun_dp()
 {
     long long i,j;
     //动态规划前初始化,只有一个体积为0的物品，可以装入容量为0的背包，容量大于0的背包方案数为0
     Bo[p][0]=1;
     for(i=1;i<n;i++)//有体积为1到n-1的n-1种物品
     {
         p=1-p;//p如果是0变换成1，如果是1变换成0
         for(j=0;j<=i*(i+1)/2;j++)//背包容量从0到 i*(i-1)/2
         {
             if(i<j || i==j)
             {
                 Bo[p][j] = (Bo[1-p][j] + Bo[1-p][j-i]) % MOD;
             }else{
                 Bo[p][j] = Bo[1-p][j];
             }
         }
     }
 }
 int fun_sum()
 {
     long long count=0,i;
     long long temp;
     for(i=0;i<=all;i++)
     {
         temp = s - i*a + (all - i)*b;
         if(temp%n == 0)
         {
             count = (count+Bo[p][i])%MOD;
         }
     }
     return count;
 }
 int main()
 {
     long long count;
     cin >> n >> s >> a >> b;
     all = n*(n-1)/2; //最多可以增加多少个a（背包容量最大值）
     fun_dp();//进行动态规划的函数
     count = fun_sum();//统计总数
     cout << count;
     return 0;
 }