hszxoj 货车运输 [lca]
题目链接: hszxoj 货车运输
题目描述与思路
- 简化题目:
求 \(x\)到 \(y\) 两点间路径的边权最小值的最大值 - 与之前的最短路最大的不同是这道题是多源最短路,那么 \(spfa\) 就废了,\(Floyd\) 定会 \(TLE\) 所以就需要用新的算法。
- 用 \(lca\) 一定是在树上的,但明显这玩意他既有环又有森林,直接用就会 \(RE\)
- 所以我们需要用到 \(kru\) 重构树
首先展示 \(kru\) 代码
void kru()
{
stable_sort(e+1,e+1+m,cmp);
cnt=n;
for(int i=1;i<=m;i++)
{
int a=find(e[i].x),b=find(e[i].y);
if(a==b) continue;
f[a]=f[b]=++cnt;
g[a].push_back(cnt),g[cnt].push_back(a),
g[b].push_back(cnt),g[cnt].push_back(b);
w[cnt]=e[i].w;
if(++tot==n-1) break;
}
root=n+tot;
}
- 首先排序一下,注意这道题是 \(最大生成树\) ,所以从大到小排序,这样求出来才是最小值的最大值,不然就是最大值的最小值了
- 有三个重要点
- \(1.\) 和正常的最小生成树不同,我们最后只需要输出两点的最近公共祖先的点权,但我们实则求的是对应的边权,就需要将边权转换为点权。不妨将相连的两点 \(x\),\(y\) 中间插入一个点,让这个点的点权为 \(x,y\) 的边权,并使这个点成为 \(x\) 和 \(y\) 的祖先
- 为什么让他成为这两个点的祖先也是显而易见的,我们最后输出最近公共祖先的权值,只有类似这个新点的权值,他才不是 \(0\),看完全部代码后会理解得更清晰
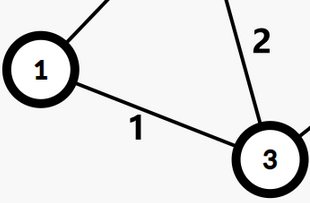
\(变化后是这样,5是新的点,5的权值为1\)
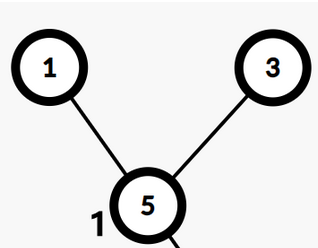
- 为什么让他成为这两个点的祖先也是显而易见的,我们最后输出最近公共祖先的权值,只有类似这个新点的权值,他才不是 \(0\),看完全部代码后会理解得更清晰
- \(2.\) 我们需要搞出来树根 \(root\) 代码里最后有一行 \(root=n+tot\) 为什么这么做呢?他重构树之后显然是有 \(森林\) 的,但他最后一个点不可能是森林(不然他无父无母的都遍历不到这个点),相当重要的,否则只有15分,后面 \(dfs\) 时有用
- \(3.\) 某个脑残问题,看到那个 \(break\) 没有,改成 \(return\) ,\(root\) 就没了 \(\large{qwq}\)
- \(1.\) 和正常的最小生成树不同,我们最后只需要输出两点的最近公共祖先的点权,但我们实则求的是对应的边权,就需要将边权转换为点权。不妨将相连的两点 \(x\),\(y\) 中间插入一个点,让这个点的点权为 \(x,y\) 的边权,并使这个点成为 \(x\) 和 \(y\) 的祖先
- 然后快乐的打完 \(lca\) 就完事了,最后输出两点最近公共祖先的权值即可,题中有一个若两点无法到达,输出 \(-1\) ,判断一下他们两个是不是在一个并查集里,如果不是自然就是不通
- 并查集如果用我这种方法别忘了 \(初始化\),初始化时要搞到 \(n+m\) ,因为我们是要建新的点的不然会炸内存
代码呈上
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=5e5+1;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=1;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,m,q,cnt,root,tot;
int w[N],f[N],fa[N],dep[N],sz[N],son[N],top[N];
vector<int>g[N];
struct aa{int x,y,w;}e[N];
bool cmp(aa s1,aa s2){return s1.w>s2.w;}
int find(int x)
{
if(f[x]!=x) f[x]=find(f[x]);
return f[x];
}
void kru()
{
stable_sort(e+1,e+1+m,cmp);
cnt=n;
for(int i=1;i<=m;i++)
{
int a=find(e[i].x),b=find(e[i].y);
if(a==b) continue;
f[a]=f[b]=++cnt;
g[a].push_back(cnt),g[cnt].push_back(a),
g[b].push_back(cnt),g[cnt].push_back(b);
w[cnt]=e[i].w;
if(++tot==n-1) break;
}
root=n+tot;
}
void dfs1(int x,int t)
{
fa[x]=t,dep[x]=dep[t]+1,sz[x]=1;
for(int y:g[x])
if(y!=t)
{
dfs1(y,x);
sz[x]+=sz[y];
if(sz[son[x]]<sz[y]) son[x]=y;
}
}
void dfs2(int x,int t)
{
top[x]=t;
if(!son[x]) return ;
dfs2(son[x],t);
for(int y:g[x])
if(y!=son[x]&&y!=fa[x])
dfs2(y,y);
}
int lca(int x,int y)
{
for(;top[x]!=top[y];x=fa[top[x]])
if(dep[top[x]]<dep[top[y]]) swap(x,y);
return dep[x]<dep[y]?x:y;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
int x,y;
read(n),read(m);
for(int i=1;i<=n+m;i++) f[i]=i;
for(int i=1;i<=m;i++)
read(e[i].x),read(e[i].y),read(e[i].w);
kru(),dfs1(root,0),dfs2(root,root);
read(q);
while(q--)
read(x),read(y),
cout<<((find(x)!=find(y))?-1:w[lca(x,y)])<<endl;
}
并查集还可以这么打(虽然大多数人都是这么打的)
int find(int x)
{
return (!f[x])?x:f[x]=find(f[x]);
}
这样就不需要初始化了
hszxoj 货车运输 [lca]的更多相关文章
- NOIP2013货车运输[lca&&kruskal]
题目描述 A 国有 n 座城市,编号从 1 到 n,城市之间有 m 条双向道路.每一条道路对车辆都有重量限制,简称限重.现在有 q 辆货车在运输货物, 司机们想知道每辆车在不超过车辆限重的情况下,最多 ...
- NOIP2013 货车运输 LCA倍增+最大生成树
#include <cstdio> #include <iostream> #include <ctime> #include <vector> #in ...
- 洛谷 P1967 货车运输 LCA + 最小生成树
两点之间边权最大值的最小值一定在图的最小生成树中取到. 求出最小生成树,进行倍增即可. Code: #include<cstdio> #include<algorithm> u ...
- NOIP2013 货车运输 (最大生成树+树上倍增LCA)
死磕一道题,中间发现倍增还是掌握的不熟 ,而且深刻理解:SB错误毁一生,憋了近2个小时才调对,不过还好一遍AC省了更多的事,不然我一定会疯掉的... 3287 货车运输 2013年NOIP全国联赛提高 ...
- Codevs 3287 货车运输 2013年NOIP全国联赛提高组(带权LCA+并查集+最大生成树)
3287 货车运输 2013年NOIP全国联赛提高组 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 传送门 题目描述 Description A 国有 n 座 ...
- 「NOIP2013」「LuoguP1967」货车运输(最大生成树 倍增 LCA
题目描述 AA国有nn座城市,编号从 11到nn,城市之间有 mm 条双向道路.每一条道路对车辆都有重量限制,简称限重.现在有 qq 辆货车在运输货物, 司机们想知道每辆车在不超过车辆限重的情况下,最 ...
- 洛谷P3379lca,HDU2586,洛谷P1967货车运输,倍增lca,树上倍增
倍增lca板子洛谷P3379 #include<cstdio> struct E { int to,next; }e[]; ],anc[][],log2n,deep[],n,m,s,ne; ...
- codevs3287货车运输(最小生成树+LCA)
3287 货车运输 2013年NOIP全国联赛提高组 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题目描述 Description A 国有 ...
- NOIP 2013 货车运输【Kruskal + 树链剖分 + 线段树 】【倍增】
NOIP 2013 货车运输[树链剖分] 树链剖分 题目描述 Description A 国有 n 座城市,编号从 1 到 n,城市之间有 m 条双向道路.每一条道路对车辆都有重量限制,简称限重.现在 ...
- C++之路进阶——codevs3287(货车运输)
3287 货车运输 2013年NOIP全国联赛提高组 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题目描述 Description A 国有 n ...
随机推荐
- WPF学习 - 动画基础(2)
上一篇文章粗略的介绍了一下Animation类.本篇介绍一下Storyboard. Storyboard,姑且翻译成"故事板"吧.实际上它是一个Animation对象的容器,可以容 ...
- 利用BGP Anycast 实现DNS 服务的高可用测试
一.背景 根据当前某公司内部生产系统容器平台架构设计,在各生产线边缘机房部署容器平台,与数据中心容器平台形成纵向冗余,在此情况下,传统部署在数据中心机房的DNS系统成为容器平台业务服务的短板, ...
- Solution Set -「ARC 109」
「ARC 109A」Hands Link. 讨论即可,除了煞笔出题人写了个死马的题面. #include<cstdio> #include<algorithm> using n ...
- C#开源、功能强大、免费的Windows系统优化工具 - Optimizer
前言 今天给大家推荐一款由C#开源.功能强大.免费的Windows系统优化工具 - Optimizer. 工具介绍 Optimizer是一款功能强大的Windows系统优化工具,可帮助用户提高计算机性 ...
- Django框架项目之git笔记——版本控制器、git介绍、git使用
文章目录 版本控制器 git 简介 git与svn比较 git的工作流程 版本库间的通信 git分支管理 git使用 流程(核心总结) 安装 基础命令 将已有的文件夹 - 初始化为git仓库 在指定目 ...
- C++在HotSpot VM中一种巧妙的内存管理方式
在HotSpot VM中定义了一个Relocation类及相关的子类,可以通过这些类操作不同的重定位数据,如在CodeCache中读写这些数据.这些类需要的内存很小,但是不同的类需要的内存大小又不一样 ...
- Gossip in Hyperledger Fabric
1. Gossip协议基础 1.1 什么是分布式系统 分布式系统(Distributed System)是由多台计算机或计算节点组成的计算机系统,这些计算节点通过网络连接在一起,并协同工作以完成共同的 ...
- Skywalking APM监控系列(一丶.NET5.0+接入Skywalking监听)
前言 新项目采用的abp vnext的微服务模块化架构,所以把应用的服务拆成了很多独立模块 在初期,我们通过日志还能跟踪到问题, 后期服务越来越多(大约扩充到了十几个),随着调用链路越来越深 ,问题也 ...
- 关于Android Stuido2.3和Eclipse4.4
近3年没有做Android开发了,当时用是ECLISPE电脑配置2g,用的还可以. 现在又重新开始做安卓程序,发现大家都用AS了,作为技术人员,也就开始用了. (几年前AS已经发布,不过是0.x版本, ...
- 红瞳瞳CRUD Avue各参数作用
常用的两个avue文档: avue 开发文档: https://www.bookstack.cn/read/avue-2.x/3c22e1c01099c1f1.md avue开发指南:https: ...
