Bresenham算法

1 算法原理

基本原理从某处摘得：设直线方程为y_i+1=y_i+k(x_i+1-x_i)+k。假设列坐标象素已经确定为x_i，其行坐标为y_i。那么下一个象素的列坐标为x_i＋1，而行坐标要么为y_i，要么递增1为y_i＋1。是否增1取决于误差项d的值。误差项d的初值d₀＝0，x坐标每增加1，d的值相应递增直线的斜率值k，即d＝d＋k。一旦d≥1，就把它减去1，这样保证d在0、1之间。当d≥0.5时，直线与垂线x=x_i＋1交点最接近于当前象素(x_i，y_i)的右上方象素(x_i＋1，y_i＋1)；而当d<0.5时，更接近于右方象素(x_i＋1，y_i)。为方便计算，令e＝d－0.5，e的初值为－0.5，增量为k。当e≥0时，取当前象素(x_i，y_i)的右上方象素(x_i＋1，y_i＋1)；而当e<0时，取(x_i，y_i)右方象素(x_i＋1，y_i)。

由于显示直线的像素点只能取整数值坐标,可以假设直线上第i个像素点的坐标为(X_i,Y_i),它是直线上点(X_i,Y_i)最佳近似,并且X_i=X_i(假设m<1),如下图所示.那么直线上下一个像素点的可能位置是(X_i+1,Y_i)或者(X_i+1,Y_i+1).

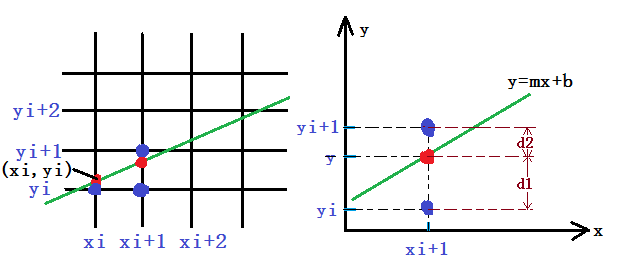
由图可知：在x=X_i+1处，直线上的点y的值是：y=m(X_i+1)+b，该点离像素点(X_i+1,Y_i)和像素点(X_i+1,Y_i+1)的距离分别为d1和d2。

　　　　d1 = Y - Y_i = m(X_i+1)+b - Y_i;　　　　(1)

　　　　d2 = (Y_i+1) - Y = (Y_i+1) - m(X_i+1) - b;　　　　(2)

　　　　两个距离的差是：

　　　　d1-d2 = 2m(X_i+1) - 2Y_i + 2b -1;　　　　(3)

　　对于公式(3)：

　　a：当此值为正时，d1>d2,说明直线上理论点离(X_i+1,Y_i+1)像素较近，下一个像素点应取(X_i+1,Y_i+1)；

　　b：当此值为负时，d1<d2,说明直线上理论点离(X_i+1,Y_i)像素较近，下一个像素点赢取(X_i+1,Y_i)；

　　c：当此值为零时，d1=d2,说明直线上理论点离上、下两个像素点的距离相等，取那个点都行，假设算法规定这种情况下取(X_i+1,Y_i+1)作为下一个像素点。

　　因此只要利用(d1-d2)的符号就可以决定下一个像素点的选择。需进一步定义一个判别式：

　　P_i = △X × (d1-d2) = 2△Y·X_i - 2△X·Y_i + c 　　　(4)

　　　　其中△X=(X2-X1)>0，因此P_i与(d1-d2)有相同的符号；

　　　　△Y=Y2-Y1；m=△Y/△X；c=2△Y+△X(2b-1)

　　对(4)进一步处理得出误差判别递推公式并消除常数c；

　　将(4)中的下标i改为i+1，得到：

　　P_i+1 = △X × (d1-d2) = 2△Y·X_i+1 - 2△X·Y_i+1 + c　　(5)

　　假设直线的初始端点恰好是其像素点的坐标，即满足：

　　Y1 = mX1 + b ;　　(6)

　　由公式(4)和(6)得到p1的初始值：

　　P1 = 2△Y - △X；　　(7)

/*推导过程*/
Pi = △X × (d1-d2) = △Y·Xi - △X·Yi + c   ()
Y1 = mX1 + b                                       ()

P1 =  △Y·X1 - △X·Y1 + c
    = △Y·X1 - △X·(△Y/△X·X1+b) + c
    = △Y·X1 - △Y·X1 - △X·b + c
    = c - △X·b
    = △Y+△X(2b-) - △X·b
    = △Y - △X

　　所以可以用误差判别变量，得到如下算法表示：

　　初始：P1 = 2△Y - △X　　(8)

　　当P_i>=0时：Y_i+1 = Y_i + 1,X_i+1 = X_i + 1,P_i+1 = P_i + 2(△Y-△X)[根据公式(4)和(5)得出]；

/*推导过程*/
    Pi = △X × (d1-d2) = △Y·Xi - △X·Yi + c              ()
Pi+1 = △X × (d1-d2) = △Y·Xi+1 - △X·Yi+1 + c      ()

 ()-()得：

 Pi+1 = Pi + (△Y·Xi+1)-△Y·Xi - (△X·Yi+1)+△X·Yi 

∵ Pi> 时 Yi+1 = Yi + ,Xi+1 = Xi +
∴ Pi+1 =  Pi + (△Y·(Xi + ))-△Y·Xi - (△X·(Yi + ))+△X·Yi
           = Pi + (△Y-△X)

　　否则：Y_i+1 = Y_i,X_i+1=X_i + 1,P_i+1=P_i+2△y[根据公式(4)和(5)得出]

/*推导过程*/
    Pi = △X × (d1-d2) = △Y·Xi - △X·Yi + c              ()
    Pi+1 = △X × (d1-d2) = △Y·Xi+1 - △X·Y(i+1) + c      ()

 ()-()得：

 Pi+1 = Pi + (△Y·Xi+1)-△Y·Xi - (△X·Yi+1)+△X·Yi 

∵ Pi> 时 Yi+1 = Yi,Xi+1 = Xi +
∴ Pi+1 =  Pi + (△Y·(Xi + ))-△Y·Xi - (△X·(Yi))+△X·Yi
           =  Pi + △Y

　　从(8)式可以看出，第i+1步的判别变量P_i+1仅与第i步的判别变量P_i、直线的两个端点坐标分量差△X和△Y有关，运算中只含有整数相加和乘2运算，而乘2可利用算术左移一位来完成，因此这个算法速度快并易于硬件实现。