c语言数字图像处理（三）：仿射变换

仿射变换及坐标变换公式

几何变换改进图像中像素间的空间关系。这些变换通常称为橡皮模变换，因为它们可看成是在一块橡皮模上印刷一幅图像，然后根据预定的一组规则拉伸该薄膜。在数字图像处理中，几何变换由两个基本操作组成：

(1)坐标的空间变换

(2)灰度内插，即对变换后的像素赋灰度值

　　坐标变换公式

(x,y) = T{(v, w)}

其中，(v, w)是原图像中像素的坐标，(x, y)是变换后图像中像素的坐标。最常用的空间坐标变换之一是仿射变换

基于上式的仿射变换公式

实际上，我们可以用两种方法来使用上式。第一种方法称为向前映射，它由扫描输入图像的像素，并在每个位置(v, w)用上式直接计算输出图像中相应像素的空间位置(x, y)组成。向前映射算法的一个问题是输入图像中的两个或更多个像素可被变换到输出图像的同一位置，这就产生了如何把多个输出值合并到一个输出像素的问题。第二种方法，反向映射，扫描输出像素的位置，并在每一个位置(x, y)使用(v, w) = T^-1(x, y)计算输入图像中的相应位置。然后通过内插决定输出像素的灰度值。本篇文章使用反向映射。

<以上基础知识来源于 《数字图像处理》冈萨雷斯 P50-P51 读者可自行查阅>

在上一篇文章中，主要是图片的放大与缩小，在灰度内插的过程中也涉及到目标图像到原图像的坐标变换，代码如下

 void bilinera_interpolation(short** in_array, short height, short width,
                             short** out_array, short out_height, short out_width)
 {
     double h_times = (double)out_height / (double)height,
            w_times = (double)out_width / (double)width;
     short  x1, y1, x2, y2, f11, f12, f21, f22;
     double x, y;

     for (int i = ; i < out_height; i++){
         for (int j = ; j < out_width; j++){
             x = j / w_times;
             y = i / h_times;
             x1 = (short)(x - );
             x2 = (short)(x + );
             y1 = (short)(y + );
             y2 = (short)(y - );
             f11 = is_in_array(x1, y1, height, width) ? in_array[y1][x1] : ;
             f12 = is_in_array(x1, y2, height, width) ? in_array[y2][x1] : ;
             f21 = is_in_array(x2, y1, height, width) ? in_array[y1][x2] : ;
             f22 = is_in_array(x2, y2, height, width) ? in_array[y2][x2] : ;
             out_array[i][j] = (short)(((f11 * (x2 - x) * (y2 - y)) +
                                        (f21 * (x - x1) * (y2 - y)) +
                                        (f12 * (x2 - x) * (y - y1)) +
                                        (f22 * (x - x1) * (y - y1))) / ((x2 - x1) * (y2 - y1)));
         }
     }
 }

其中，第11，12行为目标图像到原图像的坐标变换，接下来根据仿射变换公式对图像做进一步处理

水平偏移变换

水平偏移变换公式为

x = v

y = Sh * v + w

反解上述公式得

v = x

w = y - Sh * v

结果为目标图像到原图像的坐标变换，令Sh = 0.5，并对应用到上述代码11，12行，同时将图像扩大到2800*1280，结果为

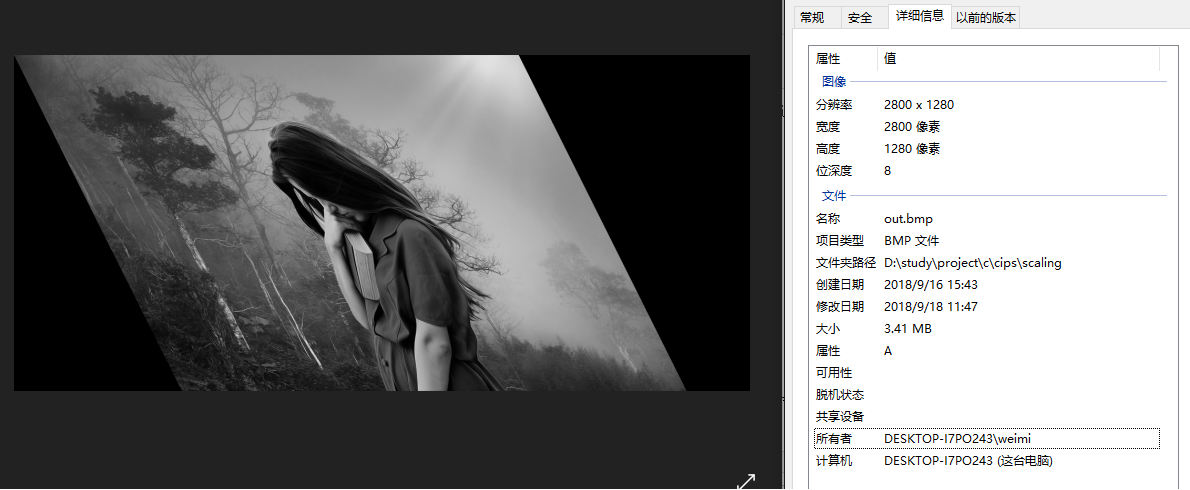
旋转变换

旋转变换公式

x = vcosθ - wsinθ

y = vsinθ + wcosθ

令θ = ∏/4，反解得

v = x/√2 + y/√2

w = y/√2 - x/√2

将图像扩大为2000*2000，但是这个时候得到的图像为

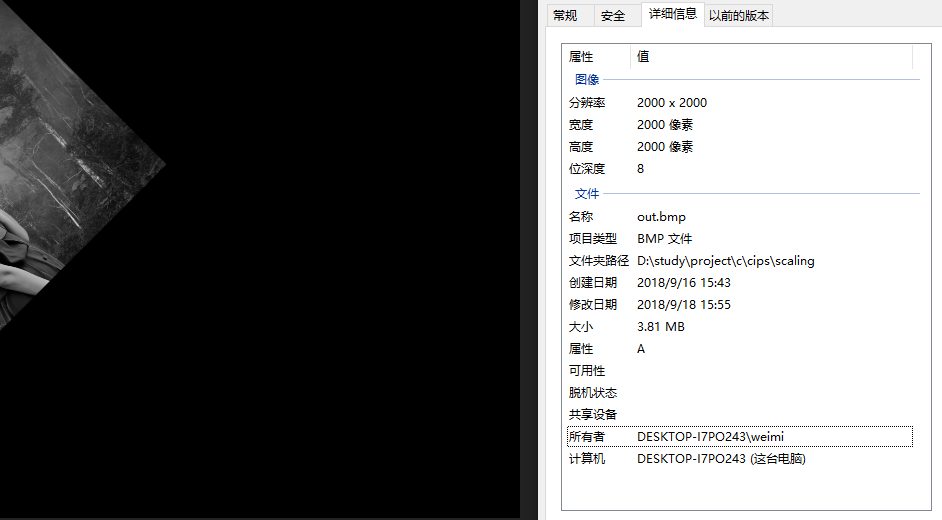
为了解决这一问题，使旋转后的图像位于中央，我将所得图片右移m_w, 下移m_h，则公式变为

x = vcosθ - wsinθ + m_w

y = vsinθ + wcosθ + m_h

令θ = ∏/4，反解得

v = (x + y - m_h - m_w)/√2

w = (y - x - m_h + m_w)/√2

结果为

其余变换原理基本相同，因此不再进行演示