JavaScript图形实例：正弦曲线

正弦曲线的坐标方程为：

Y=A*SIN(X) （A为振幅）

1．正弦曲线

在弧度为0~4π的正弦曲线上取360个点，将这些点用线连接起来，可以绘制出正弦曲线。编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>正弦曲线的绘制</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.strokeStyle="red";

context.lineWidth=2;

var dig=Math.PI/90;

context.beginPath();

for (var x=0;x<360;x++)

{

y=150-120*Math.sin(x*dig);

if (x==0)

{

context.moveTo(x,y);

}

else

context.lineTo(x,y);

}

context.stroke();

}

</script>

</head>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出一条正弦曲线，如图1所示。

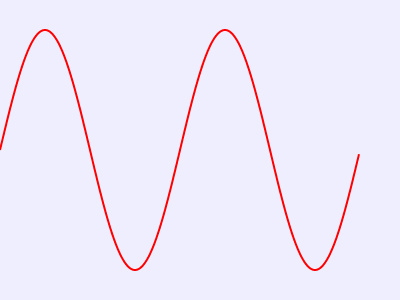
图1 正弦曲线

若将上述文件中的语句“y=150-120*Math.sin(x*dig);”改为“y=150-120*Math.cos(x*dig);”，可以绘制出如图2所示的余弦曲线。

图2 余弦曲线

2．正弦波

适当减小图1中正弦函数的振幅，并且用循环绘制多条在Y轴方向上向下平移若干单位的正弦曲线，可以绘制出正弦波形图案。编写如下的HTML文件。

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.strokeStyle="red";

context.lineWidth=2;

var dig=Math.PI/90;

context.beginPath();

for (py=40;py<=200;py+=5)

for (var x=0;x<360;x++)

{

y=py-15*Math.sin(x*dig-dig*(py-40)/2); // 正弦函数的相位进行变化

if (x==0)

{

context.moveTo(x,y);

}

else

context.lineTo(x,y);

}

context.stroke();

}

</script>

</head>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出正弦波形，如图3所示。

图3 正弦波形

3．合成正弦波形

若将正弦函数进行合成，例如取 Y=A*SIN(3X)*SIN(X)，可以绘制出合成正弦波图案。

编写的HTML代码如下。

<!DOCTYPE html>

<head>

<title>合成正弦波</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.strokeStyle="red";

context.lineWidth=2;

var dig=Math.PI/90;

context.beginPath();

for (py=40;py<=200;py+=5)

for (var x=0;x<360;x++)

{

y=py-15*Math.sin(3*x*dig)*Math.sin(x*dig-dig*(py-40)/2);

if (x==0)

{

context.moveTo(x,y);

}

else

context.lineTo(x,y);

}

context.stroke();

}

</script>

</head>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出合成正弦波图案，如图4所示。

图4 合成正弦波

4．端点按三角函数规律变化的线段

将线段的端点按三角函数规律变化，可绘制图形。例如，将线段的一个端点取自正弦曲线，另一个端点取自对应的余弦曲线，可以编写HTML文件如下。

<!DOCTYPE html>

<head>

<title>端点按三角函数规律变化的线段</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.strokeStyle="blue";

context.lineWidth=1;

var dig=Math.PI/90;

context.beginPath();

context.moveTo(0,150);

for (var i=0;i<360;i++)

{

y=150-120*Math.sin(i*dig);

context.lineTo(i,y);

}

context.stroke();

context.strokeStyle="red";

context.lineWidth=2;

context.beginPath();

for (var i=0;i<360;i+=5)

{

x=150-120*Math.sin(i*dig);

y=150-120*Math.cos(i*dig);

context.moveTo(i,x);

context.lineTo(i,y);

}

context.stroke();

}

</script>

</head>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图5所示的图案。

图5 端点按三角函数规律变化的线段

将图5中绘制的线段按规律进行着色，并适当改变线段端点的三角函数计算方法。编写如下的HTML文件。

<!DOCTYPE html>

<head>

function draw(id)

{

var colors = ['red','orange', 'yellow', 'green', 'cyan','blue', 'purple' ];

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,600,200);

context.lineWidth=3;

var dig=Math.PI/150

for (var i=0;i<600;i+=4)

{

y1=100-80*Math.cos(i*dig);

y2=120-75*Math.sin(i*dig-Math.PI/2);

context.beginPath();

context.moveTo(i,y1);

context.lineTo(i+20,y2);

context.closePath();

context.strokeStyle=colors[(i/4)%7];

context.stroke();

}

</script>

</head>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图6所示的彩带图案。

图6 彩带

继续仿照图5线段图形绘制的方法，我们适当构造线段端点位置计算的三角函数，可以绘制出飘逸的丝带图案。编写如下的HTML文件。

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.strokeStyle="red";

context.lineWidth=1;

context.beginPath();

for (i=0;i<=180;i++)

{

a=i*Math.PI/360;

x1=200+180*Math.cos(1.5*a);

x2=200+180*Math.cos(2*a);

y1=150+120*Math.sin(7*a)*Math.cos(a/2.5);

y2=y1;

context.moveTo(x1,y1);

context.lineTo(x2,y2);

}

context.closePath();

context.stroke();

}

</script>

</head>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图7所示的丝带图案1。

图7 丝带图案1

改变绘制图7的HTML文件中的线段端点计算函数，编写如下的HTML文件。

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.strokeStyle="red";

context.lineWidth=1;

context.beginPath();

for (i=0;i<=300;i++)

{

a=i*Math.PI/120;

x1=200+180*Math.cos(0.5*a);

x2=200+180*Math.cos(0.5*a+Math.PI/4);

y1=150+(50-80*Math.sin(2.5*a))*Math.cos(a/2.5);

y2=150+(50-80*Math.sin(2.5*a-Math.PI/4))*Math.cos(a/2.5);

context.moveTo(x1,y1);

context.lineTo(x2,y2);

}

context.closePath();

context.stroke();

}

</script>

</head>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图8所示的丝带图案2。

图8 丝带图案2