ZOJ-1654 Place the Robots---二分图最小点覆盖+构图

题目链接：

https://vjudge.net/problem/ZOJ-1654

题目大意：

有一个N*M(N,M<=50)的棋盘，棋盘的每一格是三种类型之一：空地、草地、墙。机器人只能放在空地上。在同一行或同一列的两个机器人，若它们之间没有墙，则它们可以互相攻击。问给定的棋盘，最多可以放置多少个机器人，使它们不能互相攻击。

解题思路：

和POJ-2226类似

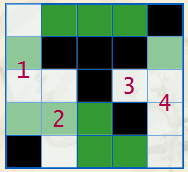
我们将每一行，每一列被墙隔开，且包含空地的连续区域称作“块”。显然，在一个块之中，最多只能放一个机器人，我们把这些块编上号。同样，把竖直方向的块也编上号。如下图：

 

       

 

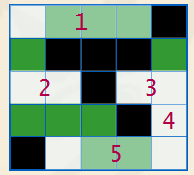
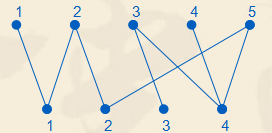
把每个横向块看作X部的点，竖向块看作Y部的点，若两个块有公共的空地，则在它们之间连边。于是，问题转化成这样的一个二分图：

 

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<queue>
 using namespace std;
 typedef pair<int, int> Pair ;
 typedef long long ll;
 const int INF = 0x3f3f3f3f;
 const int maxn =  + ;
 vector<int>G[maxn];
 int cx[maxn], cy[maxn];
 int cntx, cnty;
 bool vis[maxn];

 void init(int n)
 {
     for(int i = ; i <= n; i++)G[i].clear();
 }
 bool dfs(int u)
 {
     for(int i = ; i < G[u].size(); i++)
     {
         int v = G[u][i];
         if(!vis[v])
         {
             vis[v] = ;
             if(cy[v] == - || dfs(cy[v]))
             {
                 cx[u] = v;
                 cy[v] = u;
                 return true;
             }
         }
     }
     return false;
 }

 int maxmatch()
 {
     memset(cx, -, sizeof(cx));
     memset(cy, -, sizeof(cy));
     int ans = ;
     for(int i = ; i <= cntx; i++)
     {
         if(cx[i] == -)
         {
             memset(vis, , sizeof(vis));
             ans += dfs(i);
         }
     }
     return ans;
 }
 char Map[][];
 int T, n, m, cases;
 void build_Map()
 {
     //横向标号
     int a[][], b[][];
     memset(a, , sizeof(a));
     memset(b, , sizeof(b));
     cntx = cnty = ;
     for(int i = ; i < n; i++)
     {
         for(int j = ; j < m; j++)
         {
             if(Map[i][j] == 'o')
             {
                 a[i][j] = ++cntx;
                 j++;
                 while(j < m && Map[i][j] != '#')
                     a[i][j] = a[i][j - ], j++;
             }
         }
     }
     //竖向编号
     for(int j = ; j < m; j++)
     {
         for(int i = ; i < n; i++)
         {
             if(Map[i][j] == 'o')
             {
                 b[i][j] = ++cnty;
                 i++;
                 while(i < n && Map[i][j] != '#')
                     b[i][j] = b[i - ][j], i++;
             }
         }
     }
     init(cntx);//初始化Map
     for(int i = ; i < n; i++)
         for(int j = ; j < m; j++)
         if(Map[i][j] == 'o')G[a[i][j]].push_back(b[i][j]);
 }
 int main()
 {

     cin >> T;
     while(T--)
     {
         cin >> n >> m;
         for(int i = ; i < n; i++)cin >> Map[i];
         build_Map();
         printf("Case :%d\n", ++cases);
         cout<<maxmatch()<<endl;
     }
     return ;
 }