poj 1037 A decorative fence

题目链接：http://poj.org/problem?id=1037

Description

Richard just finished building his new house. Now the only thing the house misses is a cute little wooden fence. He had no idea how to make a wooden fence, so he decided to order one. Somehow he got his hands on the ACME Fence Catalogue 2002, the ultimate resource on cute little wooden fences. After reading its preface he already knew, what makes a little wooden fence cute. 
A wooden fence consists of N wooden planks, placed vertically in a row next to each other. A fence looks cute if and only if the following conditions are met: 
�The planks have different lengths, namely 1, 2, . . . , N plank length units. 
�Each plank with two neighbors is either larger than each of its neighbors or smaller than each of them. (Note that this makes the top of the fence alternately rise and fall.) 
It follows, that we may uniquely describe each cute fence with N planks as a permutation a1, . . . , aN of the numbers 1, . . . ,N such that (any i; 1 < i < N) (ai − ai−1)*(ai − ai+1) > 0 and vice versa, each such permutation describes a cute fence. 
It is obvious, that there are many dierent cute wooden fences made of N planks. To bring some order into their catalogue, the sales manager of ACME decided to order them in the following way: Fence A (represented by the permutation a1, . . . , aN) is in the catalogue before fence B (represented by b1, . . . , bN) if and only if there exists such i, that (any j < i) aj = bj and (ai < bi). (Also to decide, which of the two fences is earlier in the catalogue, take their corresponding permutations, find the first place on which they differ and compare the values on this place.) All the cute fences with N planks are numbered (starting from 1) in the order they appear in the catalogue. This number is called their catalogue number. 

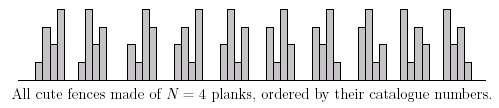
After carefully examining all the cute little wooden fences, Richard decided to order some of them. For each of them he noted the number of its planks and its catalogue number. Later, as he met his friends, he wanted to show them the fences he ordered, but he lost the catalogue somewhere. The only thing he has got are his notes. Please help him find out, how will his fences look like.

Input

The first line of the input file contains the number K (1 <= K <= 100) of input data sets. K lines follow, each of them describes one input data set. 
Each of the following K lines contains two integers N and C (1 <= N <= 20), separated by a space. N is the number of planks in the fence, C is the catalogue number of the fence. 
You may assume, that the total number of cute little wooden fences with 20 planks fits into a 64-bit signed integer variable (long long in C/C++, int64 in FreePascal). You may also assume that the input is correct, in particular that C is at least 1 and it doesn抰 exceed the number of cute fences with N planks.

Output

For each input data set output one line, describing the C-th fence with N planks in the catalogue. More precisely, if the fence is described by the permutation a1, . . . , aN, then the corresponding line of the output file should contain the numbers ai (in the correct order), separated by single spaces.

Sample Input

2
2 1
3 3

Sample Output

1 2
2 3 1

这是一个典型的递归问题，学习动规是看北大的资料看懂的，搞了半天才搞定。
C[i][k][DOWN] 是S(i)中以第k短的木棒打头的DOWN方
案数,C[i][k][UP] 是S(i)中以第k短的木棒打头的UP方案数,第k短指i根中第k短

 #include <iostream>
 #include <algorithm>
 #include <cstring>
 using namespace std;
 const int UP =; const int DOWN =;
 const int MAXN = ;
 long long C[MAXN][MAXN][]; //C[i][k][DOWN] 是S(i)中以第k短的木棒打头的DOWN方案数,C[i][k][UP] 是S(i)中以第k短的木棒打头的UP方案数,第k短指i根中第k短
 void Init(int n) {
 memset(C,,sizeof(C));
 C[][][UP] = C[][][DOWN] = ;
 for( int i =  ;i <= n; ++ i )
 for( int k = ; k <= i; ++ k ) { //枚举第一根木棒的长度
 for( int M = k; M <i ; ++M ) //枚举第二根木棒的长度
 C[i][k][UP] += C[i-][M][DOWN];
 for( int N = ; N <= k-; ++N ) //枚举第二根木棒的长度
 C[i][k][DOWN] += C[i-][N][UP];
 }
 //总方案数是 Sum{ C[n][k][DOWN] + C[n][k][UP] } k = 1.. n;
 }
 void Print(int n, long long cc)
 {
 long long skipped = ; //已经跳过的方案数
 int seq[MAXN]; //最终要输出的答案
 int used[MAXN]; //木棒是否用过
 memset(used,,sizeof(used));
 for( int i = ; i<= n; ++ i ) { //依次确定每一个位置i的木棒序号
 long long oldVal = skipped;
 int k;
 int No = ; //k是剩下的木棒里的第No短的,No从1开始算
 for( k = ; k <= n; ++k ) { //枚举位置i的木棒 ，其长度为k
 oldVal = skipped;
 if( !used[k]) {
 ++ No; //k是剩下的木棒里的第No短的
 if( i ==  )
 skipped += C[n][No][UP] + C[n][No][DOWN];
 else {
 if( k > seq[i-] && ( i <= || seq[i-]>seq[i-]))
 //合法放置
 skipped += C[n-i+][No][DOWN];
 else if( k < seq[i-] &&
 (i<= || seq[i-]<seq[i-])) //合法放置
 skipped += C[n-i+][No][UP];
 }
 if( skipped >= cc )
 break;
 }
 }
 used[k] = true;
 seq[i] = k;
 skipped = oldVal;
 }
 for( int i = ;i <= n; ++i )
 if( i < n) printf("%d ",seq[i]);
 else printf("%d",seq[i]);
 printf("\n");
 }
 int main()
 {
 int T,n; long long c;
 Init();
 scanf("%d",&T);
 while(T--) {
 scanf("%d %lld",&n,&c);
 Print(n,c);
 }
 return ;
 }