JavaScript图形实例：正多边形

圆心位于坐标原点，半径为R的圆的参数方程为

X=R*COS(θ)

Y=R*SIN(θ)

在圆上取N个等分点，将这N个点首尾连接N条边，可以得到一个正N边形。

1．正多边形阵列

构造一个8行8列的正N（N为3~10）边形阵列。编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>正多边形阵列</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,400);

context.fillStyle="yellow";

context.strokeStyle="red";

context.lineWidth=1;

context.beginPath();

for (px=30;px<390;px+=45)

for (py=30;py<390;py+=45)

{

n=((px-30)/45+(py-30)/45)%8+3;

for (i=0;i<=n;i++)

{

x1=20*Math.cos(i*Math.PI*2/n);

y1=20*Math.sin(i*Math.PI*2/n);

x=px+x1;

y=py+y1;

if (i==0)

context.moveTo(x,y);

else

context.lineTo(x,y);

}

context.closePath();

context.stroke();

context.fill();

}

</script>

</head>

<canvas id="myCanvas" width="400" height="400">您的浏览器不支持canvas！

</canvas>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出正3~10边形阵列，如图1所示。

图1 正3~10边形阵列

2．边长相等的正多边形

图1中的正N边形通过在圆周上取N等分点得到的，它们的外接圆的半径均相等，但各自的边长并不相等。若要绘制出边长相等的正N边形，可以编写如下的HTML文件。

<!DOCTYPE html>

<head>

<title>边长相等的正多边形</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,300);

context.strokeStyle="blue";

context.lineWidth=2;

var x0=150;

var y0=30;

context.beginPath();

for (n=3;n<=10;n++)

{

dig=6.28318/n;

context.moveTo(x0,y0);

x=x0;

y=y0;

for(i=0;i<n;i++)

{

x=x+80*Math.cos(i*dig);

y=y+80*Math.sin(i*dig);

context.lineTo(x,y);

}

context.lineTo(x0,y0);

}

context.stroke();

}

</script>

</head>

<canvas id="myCanvas" width="400" height="300">您的浏览器不支持canvas！

</canvas>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出边长相等的正多边形（从正三角形到正十边形），如图2所示。

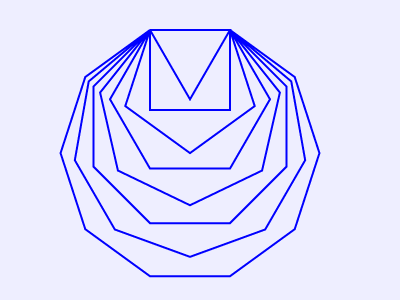
图2 边长相等的正多边形

3．漂亮的圆盘

在圆周上取N等分点，将这N个等分点两两用线段相连，共连N*(N-1)/2条边，可以绘制出圆盘图案。编写的HTML代码如下。

<!DOCTYPE html>

<head>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,400,400);

context.strokeStyle="red";

context.lineWidth=1;

var x=new Array(25);

var y=new Array(25);

var r = 180;

var n=25;

for (i = 0; i <n; i++)

{

x[i] = r * Math.cos(2 *Math.PI * i/n) + 200;

y[i] = r * Math.sin(2 *Math.PI * i/n) + 200;

}

context.beginPath();

for (i = 0; i <n-1; i++)

{

for (j = i + 1; j <n ; j++)

{

context.moveTo(x[i],y[i]);

context.lineTo(x[j],y[j]);

}

context.closePath();

context.stroke();

}

</script>

</head>

<canvas id="myCanvas" width="400" height="400">您的浏览器不支持canvas！

</canvas>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出漂亮的圆盘图案，如图3所示。

图3 圆盘图案

4．顶点在圆周上的连续线段

前面例子中，圆周上取点的参数方程的夹角θ都在0~2π之间，若将θ乘以一个参数k，可绘制出一些有趣的图形。编写的HTML文件内容如下。

<!DOCTYPE html>

<head>

<title>顶点在圆周上的连续线段</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

context.fillStyle = "cyan";

context.strokeStyle = 'red';

context.lineWidth=1;

var k=11;

var dig=Math.PI/12*k;

var radius=100;

var dx = 150;

var dy = 150;

context.beginPath();

var x = radius*Math.sin(0)+dx;

var y = radius*Math.cos(0)+dy;

context.moveTo(x,y);

for(var i = 1; i < 24; i++)

{

var x = radius*Math.sin(i * dig);

var y = radius*Math.cos(i * dig);

context.lineTo(dx+x,dy+y);

}

context.closePath();

context.fill();

context.stroke();

}

</script>

</head>

<canvas id="myCanvas" width="300" height="300">您的浏览器不支持canvas！

</canvas>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图4所示的图案。

图4 顶点在圆周上的连续线段

仿图4图形绘制的方法，我们不绘制直线，而是绘制贝塞尔曲线。编写如下的HTML文件。

<!DOCTYPE html>

<head>

<title>终点分布在圆周上的贝塞尔曲线</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEDD";

context.fillRect(0,0,300,300);

context.fillStyle = 'cyan';

context.strokeStyle = 'red';

context.globalCompositeOperation ='and';

context.lineWidth=1;

var dig=Math.PI/15*11;

var radius=100;

var dx = 150;

var dy = 150;

context.beginPath();

for(var i = 0; i < 30; i++)

{

var x = radius*Math.sin(i * dig);

var y = radius*Math.cos(i * dig);

context.bezierCurveTo(dx+x,dy+y-100,dx+x+100,dy+y,dx+x,dy+y);

}

context.closePath();

context.fill();

context.stroke();

}

</script>

</head>

<canvas id="myCanvas" width="300" height="300">您的浏览器不支持canvas！

</canvas>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出如图5所示的图案。

图5 终点分布在圆周上的贝塞尔曲线