Loj 10115 「一本通 4.1 例 3」校门外的树 (树状数组)
题目链接：https://loj.ac/problem/10115
题目描述
原题来自：Vijos P1448
校门外有很多树，学校决定在某个时刻在某一段种上一种树，保证任一时刻不会出现两段相同种类的树，现有两种操作：
- K=1，读入l,r 表示在l 到 r 之间种上一种树，每次操作种的树的种类都不同；
- K=2，读入 l,r 表示询问 l 到 r 之间有多少种树。
注意：每个位置都可以重复种树。
输入格式
第一行 表示道路总长为 n，共有 m个操作；
接下来 m 行为 m 个操作。
输出格式
对于每个 K=2 输出一个答案。
样例
样例输入
5 4
1 1 3
2 2 5
1 2 4
2 3 5
样例输出
1
2
解题思路:开始怎么想都不知道怎么维护不同段中树的种类是否相同的情况，感觉这题有个思维技巧还是挺难想的，就是我们要开两个数组，sum1分别维护左端点的数目，另一个数组sum2维护右端点的数目。这样区间[l,r]的树的种类的数目就是1-r中左端点的数目减去1-(l-1)中右端点的数目，即表示为sum1[r]-sum2[l-1]。
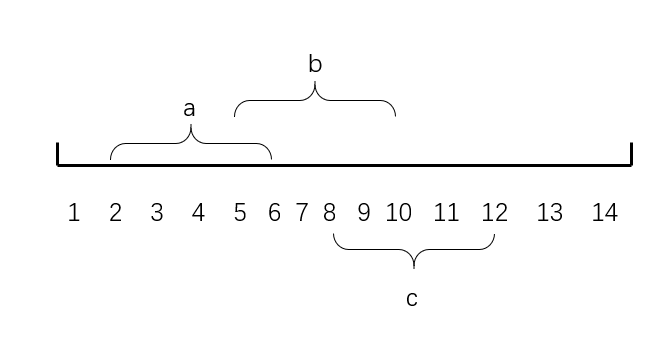
如图假如我们第一次在区间a[2,6]种上一种树，然后再在区间b[5,10]种上一种树，这时我们要统计区间c[8,12]中树的种类数目，我们就统计[1,12]中左端点的数目即 sum1[12]等于2，说明有两种树可能在给定区间内，然后我们再求区间[1,7]中右端点的数目即sum2[7-1]=1,表示有一种树完全在给定区间左边，并不是我们要求的，所以减去就好了，所以答案就为sum1[12]-sum2[7-1]了。
代码：
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<algorithm>
#include<queue>
#define mod 1000000007
using namespace std;
typedef long long ll;
const int maxn=5e4+;
int n,m,k,l,r,sum1[maxn],sum2[maxn];
//sum1[i]表示的是区间[1,i]中左端点的数目,sum2[i]表示的是区间[1,i]右端点的数目；
int lowbit(int x){return x&(-x);}
void update1(int x,int val){ //更新左端点的数目
while(x<=maxn){
sum1[x]+=val;
x+=lowbit(x);
}
}
void update2(int x,int val){ //更新右端点的数目
while(x<=maxn){
sum2[x]+=val;
x+=lowbit(x);
}
}
int ask1(int x){ //查找区间[1,x]中左端点的数目
int res=;
while(x){
res+=sum1[x];
x-=lowbit(x);
}
return res;
}
int ask2(int x){ //查找区间[1,x]中右端点的数目
int res=;
while(x){
res+=sum2[x];
x-=lowbit(x);
}
return res;
}
int main(){
cin>>n>>m;
while(m--){
cin>>k>>l>>r;
if(k==){
update1(l,); update2(r,);
}else{
cout<<ask1(r)-ask2(l-)<<endl;
}
}
return ;
}
Loj 10115 「一本通 4.1 例 3」校门外的树 (树状数组)的更多相关文章
- LOJ#10064. 「一本通 3.1 例 1」黑暗城堡
LOJ#10064. 「一本通 3.1 例 1」黑暗城堡 题目描述 你知道黑暗城堡有$N$个房间,$M$条可以制造的双向通道,以及每条通道的长度. 城堡是树形的并且满足下面的条件: 设$D_i$为如果 ...
- LOJ #10131 「一本通 4.4 例 2」暗的连锁
LOJ #10131 「一本通 4.4 例 2」暗的连锁 给一棵 \(n\) 个点的树加上 \(m\) 条非树边 , 现在需要断开一条树边和一条非树边使得图不连通 , 求方案数 . $n \le 10 ...
- LOJ#10065. 「一本通 3.1 例 2」北极通讯网络
题目链接:https://loj.ac/problem/10065 题目描述 原题来自:Waterloo University 2002 北极的某区域共有 nnn 座村庄,每座村庄的坐标用一对整数 ( ...
- LOJ#10106. 「一本通 3.7 例 2」单词游戏
题目链接:https://loj.ac/problem/10106 题目描述 来自 ICPC CERC 1999/2000,有改动. 有 NNN 个盘子,每个盘子上写着一个仅由小写字母组成的英文单词. ...
- LOJ #10132. 「一本通 4.4 例 3」异象石
题目地址 LOJ 题解 神仙思路.思路参考自<算法竞赛进阶指南>. 考虑维护dfs序中相邻两个石头的距离,那么每次?的答案就是sum/2(首尾算相邻) 然后维护一下拿个平衡树/set维护一 ...
- LOJ #10222. 「一本通 6.5 例 4」佳佳的 Fibonacci
题目链接 题目大意 $$F[i]=F[i-1]+F[i-2]\ (\ F[1]=1\ ,\ F[2]=1\ )$$ $$T[i]=F[1]+2F[2]+3F[3]+...+nF[n]$$ 求$T[n] ...
- LOJ 10138 -「一本通 4.5 例 1」树的统计
树链剖分模板题,详见这篇博客.
- LOJ 10155 - 「一本通 5.2 例 3」数字转换
前言 从现在开始,这个博客要写一些题解了.起初,开这个博客只是好玩一样,没事就写写CSS.JS,然后把博客前端搞成了现在这个样子.以前博客只是偶尔记录一些东西,刷题也从来不记录,最近受一些学长的影响, ...
- loj #10001. 「一本通 1.1 例 2」种树
题面 解题思路 贪心,首先按右端点排序,然后从小往大扫,因为要求树最少,所以要尽量放在右端点.然后开个bool数组判断是否种过树即可. 代码 #include<iostream> #inc ...
随机推荐
- Java内存模型深度解读
Java内存模型规范了Java虚拟机与计算机内存是如何协同工作的.Java虚拟机是一个完整的计算机的一个模型,因此这个模型自然也包含一个内存模型——又称为Java内存模型. 如果你想设计表现良好的并发 ...
- 在.net桌面程序中自定义鼠标光标
有的时候,一个自定义的鼠标光标能给你的程序增色不少.本文这里介绍一下如何在.net桌面程序中自定义鼠标光标.由于.net的桌面程序分为WinForm和WPF两种,这里分别介绍一下. WinForm程序 ...
- 排列组合[HDU1521]
排列组合 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submis ...
- Qt中的多线程编程
http://www.ibm.com/developerworks/cn/linux/l-qt-mthrd/ Qt 作为一种基于 C++ 的跨平台 GUI 系统,能够提供给用户构造图形用户界面的强大功 ...
- IoC容器Autofac之IOC/DI基本概念(二)
原文:http://www.cnblogs.com/xdp-gacl/p/4249939.html 1.1.IoC是什么 Ioc—Inversion of Control,即“控制反转”,一种设计思想 ...
- 绩效考核指标KPI 听课笔记
以前一直听人在说KPI,今天终于明白KPI是什么意思了!
- MAC下pyenv和pyenv-virtualenv插件初探
为什么会使用pyenv和pyenv-virtualenv插件 一般mac自带一个python版本,称为系统版本.对于开发者而言,肯定不够用啦.所以需要在同一个mac上组建不同的开发环境并且不会冲突. ...
- 【数学】NOIP数论内容整理
NOIP数论内容整理 注:特别感谢sdsy的zxy神仙以及lcez的tsr筮安帮助审稿 一.整除: 对于\(a,b~\in~Z\),若\(\exists~k~\in~Z\),\(s.t.~b~=~k~ ...
- Mycat源码中的单例模式
在MyCat的源码中,很多对象都使用到了单例模式. 首先是MycatServer类,该实例必须全局唯一,所以这里涉及到JAVA的单实例模式,就是一个类只有唯一一个实例对象存在.先来看看mycat源码是 ...
- vue属性
1. 图片地址: data:{ url:"https://www.baidu.com/img/bd_logo1.png"}, <img v-bind:src="ur ...